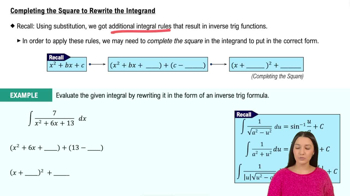
41–48. Geometry problems Use a table of integrals to solve the following problems.
46. Find the area of the region bounded by the graph of y = 1/√(x² - 2x + 2) and the x-axis from x = 0 to x = 3.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 5:23m
5:23mMaster Finding Area Between Curves on a Given Interval with a bite sized video explanation from Patrick
Start learning