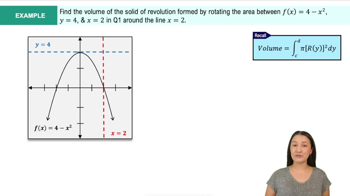
9. Graphical Applications of Integrals
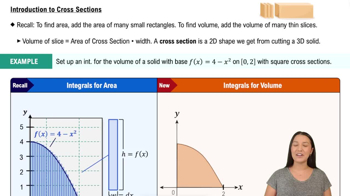
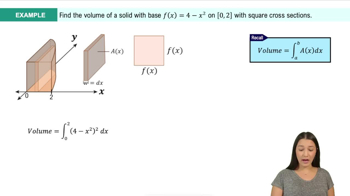
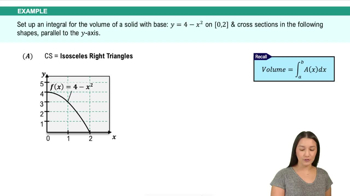
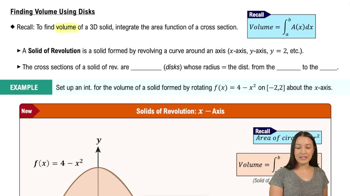
Introduction to Volume & Disk Method
Practice this topic
- Multiple Choice
Find the volume of the solid whose base is the region bounded by the function and the x-axis with square cross sections perpendicular to the x-axis.
129views6rank - Multiple Choice
Find the volume for a solid whose base is the region between the curve and the x-axis on the interval from and whose cross sections are equilateral triangles with bases parallel to the y-axis.
124views3rank - Multiple Choice
Find the volume of the solid obtained by rotating the region bounded by , , & about the x-axis.
120views3rank - Multiple Choice
Find the volume of the solid formed by revolving the area bounded by from to and the y-axis around the y-axis.
109views2rank - Textbook Question
74. Volume of a Solid
Consider the region R bounded by:
The graph of f(x) = 1/(x + 2)
The x-axis on the interval [0,3].
Find the volume of the solid formed when R is revolved about the y-axis.
13views - Textbook Question
Let f(x) = √(x + 1). Find the area of the surface generated when:
Region bounded by f(x) and the x-axis on [0, 1]
Revolved about the x-axis
15views - Textbook Question
65. Volume Find the volume of the solid generated when the region bounded by y = sin²(x) * cos^(3/2)(x) and the x-axis on the interval [0, π/2] is revolved about the x-axis.
18views - Textbook Question
87. Surface area Find the area of the surface generated when the curve f(x) = sin x on [0, π/2] is revolved about the x-axis.
17views