Use synthetic division and the Remainder Theorem to find the indicated function value. f(x)=3x3−7x2−2x+5;f(−3)
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
Dividing Polynomials
Problem 53
Textbook Question
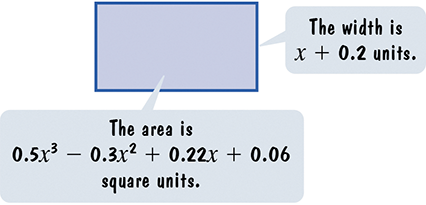
Write a polynomial that represents the length of each rectangle. Transcription: The area of the rectangle is 0.5x3 - 0.3x2 + 0.22x + 0.06 square units and its width is x + 0.2 units
 Verified step by step guidance
Verified step by step guidance1
Recall the formula for the area of a rectangle: \(\text{Area} = \text{Length} \times \text{Width}\).
Given the area as \$0.5x^{3} - 0.3x^{2} + 0.22x + 0.06\( and the width as \)x + 0.2\(, set up the equation: \)0.5x^{3} - 0.3x^{2} + 0.22x + 0.06 = \text{Length} \times (x + 0.2)$.
To find the length, divide the area polynomial by the width polynomial: \(\text{Length} = \frac{0.5x^{3} - 0.3x^{2} + 0.22x + 0.06}{x + 0.2}\).
Perform polynomial division (either long division or synthetic division) to divide \$0.5x^{3} - 0.3x^{2} + 0.22x + 0.06\( by \)x + 0.2$.
The quotient from this division will be the polynomial expression representing the length of the rectangle.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Expressions
A polynomial is an algebraic expression consisting of terms with variables raised to non-negative integer powers and coefficients. Understanding how to manipulate polynomials, including addition, subtraction, multiplication, and division, is essential for working with expressions like the given area and width.
Recommended video:
Guided course

Introduction to Algebraic Expressions
Area of a Rectangle
The area of a rectangle is found by multiplying its length by its width. Given the area and one dimension (width), you can find the other dimension (length) by dividing the area polynomial by the width polynomial.
Recommended video:
Guided course

Systems of Inequalities
Polynomial Division
Polynomial division is the process of dividing one polynomial by another, similar to numerical long division. It is used here to find the length polynomial by dividing the area polynomial by the width polynomial.
Recommended video:
Guided course

Introduction to Polynomials
Related Videos
Related Practice
Textbook Question
341
views
