Textbook Question
Find the value of the function for the given value of x. ƒ(x)=[[x]], for x=(-π)
867
views
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:
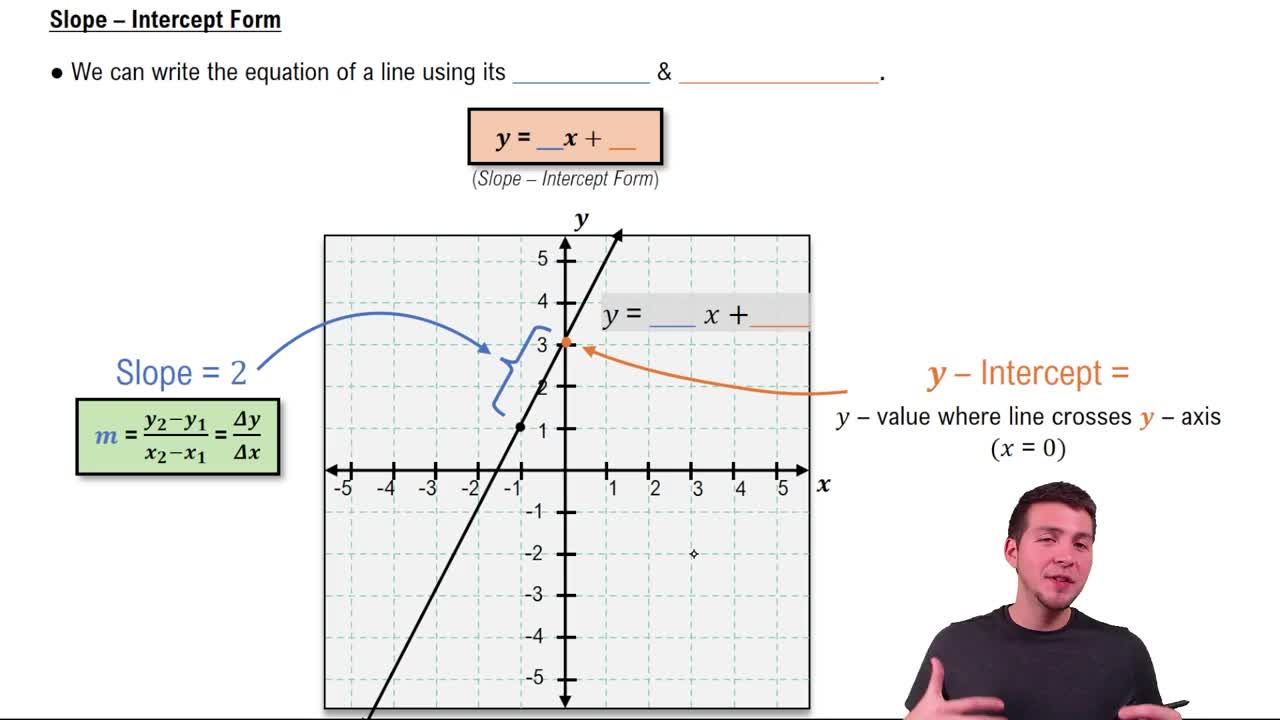


 5:28m
5:28mMaster Equations with Two Variables with a bite sized video explanation from Patrick
Start learning