In Exercises 11–18, graph each function by making a table of coordinates. If applicable, use a graphing utility to confirm your hand-drawn graph. f(x) = 4x
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
6. Exponential & Logarithmic Functions
Introduction to Exponential Functions
Problem 19
Textbook Question
In Exercises 19–24, the graph of an exponential function is given. Select the function for each graph from the following options:
f(x)=3x,g(x)=3x−1,h(x)=3x−1,f(x)=−3x,G(x)=3−x,H(x)=−3−x.
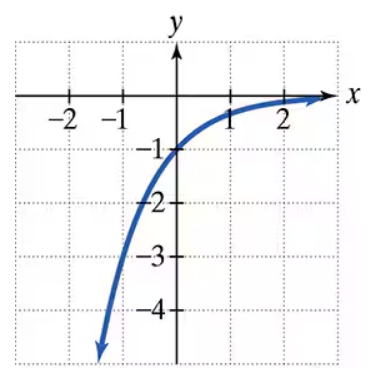
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the general shape of the graph. The graph shows exponential growth, which means the base of the exponential function is greater than 1, and the function increases as x increases.
Step 2: Check the y-intercept of the graph. The y-intercept occurs when x = 0. From the graph, observe the value of the function at x = 0.
Step 3: Compare the y-intercept to the given functions. For example, for f(x) = 3^x, the y-intercept is 3^0 = 1. For g(x) = 3^(x-1), the y-intercept is 3^{-1} = 1/3. For h(x) = 3^x - 1, the y-intercept is 1 - 1 = 0.
Step 4: Look at the behavior of the graph for negative x-values. If the graph approaches zero but never touches the x-axis, it matches the behavior of 3^x or its transformations. If the graph is reflected or shifted, it will affect this behavior.
Step 5: Based on the y-intercept and the shape, match the graph to the correct function from the options: f(x) = 3^x, g(x) = 3^(x-1), h(x) = 3^x - 1, f(x) = -3^x, G(x) = 3^{-x}, or H(x) = -3^{-x}.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Exponential Functions
An exponential function has the form f(x) = a^x, where the base a is a positive constant not equal to 1. These functions exhibit rapid growth or decay depending on the base and the exponent's sign. Understanding the general shape and behavior of exponential graphs is essential for identifying specific functions.
Recommended video:

Exponential Functions
Horizontal and Vertical Shifts
Shifts in exponential functions occur when constants are added or subtracted inside the exponent or outside the function. For example, f(x) = 3^(x-1) shifts the graph right by 1 unit, while f(x) = 3^x - 1 shifts it down by 1 unit. Recognizing these shifts helps match graphs to their corresponding equations.
Recommended video:

Shifts of Functions
Reflections and Negative Exponents
A negative sign in front of the function reflects the graph across the x-axis, while a negative exponent reflects it across the y-axis. For instance, f(x) = -3^x flips the graph vertically, and g(x) = 3^(-x) flips it horizontally. Identifying these reflections is key to distinguishing between similar exponential functions.
Recommended video:
Guided course

Zero and Negative Rules

 6:13m
6:13mWatch next
Master Exponential Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
949
views
