Give the equations of any vertical, horizontal, or oblique asymptotes for the graph of each rational function. ƒ(x)=(2x+6)/(x-4)
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
5. Rational Functions
Graphing Rational Functions
Problem 50c
Textbook Question
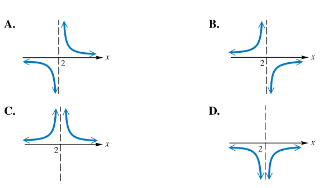
Work each problem. Choices A–D below show the four ways in which the graph of a rational function can approach the vertical line x=2 as an asymptote. Identify the graph of each rational function defined in parts (a) – (d).
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the vertical asymptote of the function. The function is given as \(ƒ(x) = -\frac{1}{x-2}\), so the vertical asymptote occurs where the denominator is zero, which is at \(x=2\).
Step 2: Analyze the behavior of the function near the vertical asymptote \(x=2\). Since the numerator is negative (-1), the function will approach positive or negative infinity depending on the side from which \(x\) approaches 2.
Step 3: Consider the limit as \(x\) approaches 2 from the left (\(x \to 2^-\)). The denominator \((x-2)\) is negative and close to zero, so \(-\frac{1}{x-2}\) becomes a large positive number (because dividing by a small negative number gives a large negative, but the negative sign in front flips it to positive). Thus, the graph goes to \(+\infty\) on the left side of \(x=2\).
Step 4: Consider the limit as \(x\) approaches 2 from the right (\(x \to 2^+\)). The denominator \((x-2)\) is positive and close to zero, so \(-\frac{1}{x-2}\) becomes a large negative number. Thus, the graph goes to \(-\infty\) on the right side of \(x=2\).
Step 5: Match this behavior to the graphs provided. The graph should show the function going to positive infinity on the left side of \(x=2\) and negative infinity on the right side of \(x=2\). This corresponds to graph A.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Vertical Asymptotes of Rational Functions
A vertical asymptote occurs where the denominator of a rational function is zero, causing the function to approach infinity or negative infinity. For the function f(x) = -1/(x-2), the vertical asymptote is at x = 2, where the function is undefined and the graph approaches a vertical line.
Recommended video:

Determining Vertical Asymptotes
Behavior Near Vertical Asymptotes
The behavior of a rational function near a vertical asymptote depends on the sign of the function on either side of the asymptote. For f(x) = -1/(x-2), as x approaches 2 from the left, the function tends to positive infinity, and from the right, it tends to negative infinity, indicating opposite behavior on each side.
Recommended video:

Determining Vertical Asymptotes
Graphing Rational Functions
Graphing rational functions involves identifying asymptotes and understanding the function's behavior near these lines. The sign and magnitude of the function near the vertical asymptote help determine which graph matches the function, as seen in the choices where the graph approaches infinity or negative infinity differently on each side of x=2.
Recommended video:
How to Graph Rational Functions

 5:31m
5:31mWatch next
Master Graphing Rational Functions Using Transformations with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
491
views
