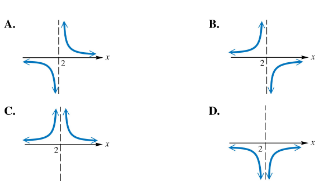
Work each problem. Choices A–D below show the four ways in which the graph of a rational function can approach the vertical line x=2 as an asymptote. Identify the graph of each rational function defined in parts (a) – (d). ƒ(x)=1/(x-2)

A rational function is a function that can be expressed as the ratio of two polynomials. The general form is ƒ(x) = P(x)/Q(x), where P and Q are polynomials. Understanding rational functions is crucial for analyzing their behavior, particularly in relation to asymptotes, which occur where the function is undefined.

Vertical asymptotes are vertical lines that represent values of x where a rational function approaches infinity or negative infinity. They occur at values of x that make the denominator zero, provided the numerator is not also zero at those points. For the function ƒ(x) = 1/(x-2), there is a vertical asymptote at x = 2.

The behavior of a graph near an asymptote is essential for understanding how the function behaves as it approaches the asymptote. As x approaches the vertical asymptote from the left or right, the function values will tend to either positive or negative infinity. This behavior helps in sketching the graph and predicting its overall shape.