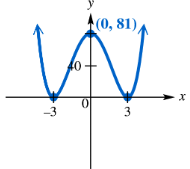
Show that the real zeros of each polynomial function satisfy the given conditions. See Example 6.
; no real zero less than -2
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 6:04m
6:04mMaster Introduction to Polynomial Functions with a bite sized video explanation from Patrick
Start learning