Begin by graphing the standard cubic function, f(x) = x³. Then use transformations of this graph to graph the given function. h(x) = (1/2)(x − 2)³ – 1
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Common Functions
Problem 43
Textbook Question
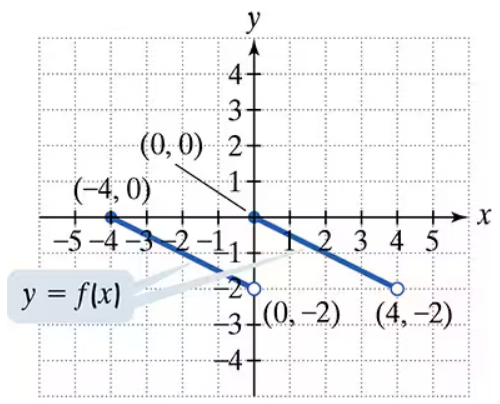
Use the graph of y = f(x) to graph each function g. g(x) = (1/2)f(2x)
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the transformations applied to the function f(x). The given function g(x) = (1/2)f(2x) involves two transformations: a horizontal compression by a factor of 2 and a vertical scaling by a factor of 1/2.
Step 2: Start with the horizontal compression. The term f(2x) indicates that the graph of f(x) is horizontally compressed by a factor of 2. This means that every x-coordinate of the points on the graph of f(x) is divided by 2.
Step 3: Apply the vertical scaling. The term (1/2)f(2x) indicates that the graph of f(2x) is vertically scaled by a factor of 1/2. This means that every y-coordinate of the points on the graph of f(2x) is multiplied by 1/2.
Step 4: Combine the transformations. To graph g(x), take each point (x, y) on the graph of f(x), apply the horizontal compression to get (x/2, y), and then apply the vertical scaling to get (x/2, y/2).
Step 5: Plot the transformed points on the graph and connect them smoothly to complete the graph of g(x). Ensure that the overall shape of the graph reflects the combined transformations.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Function Transformation
Function transformation refers to the process of altering the graph of a function through various operations, such as stretching, compressing, or shifting. In the case of g(x) = (1/2)f(2x), the function undergoes both a vertical compression by a factor of 1/2 and a horizontal compression by a factor of 2, which affects the shape and position of the graph.
Recommended video:

Domain & Range of Transformed Functions
Horizontal Scaling
Horizontal scaling involves changing the input values of a function, which affects how the graph is stretched or compressed along the x-axis. In g(x) = (1/2)f(2x), the '2x' indicates that the function f(x) is being evaluated at twice the rate, resulting in a horizontal compression of the graph by a factor of 2, making it appear narrower.
Recommended video:

Horizontal Parabolas
Vertical Scaling
Vertical scaling modifies the output values of a function, impacting the graph's height. In the function g(x) = (1/2)f(2x), the factor of 1/2 indicates that the output of f(2x) is halved, leading to a vertical compression of the graph. This means that all y-values of the function g will be half of those of f, effectively lowering the graph.
Recommended video:

Foci and Vertices of an Ellipse

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
568
views
