Table of contents

0. Review of Algebra4h 18m
1. Equations & Inequalities3h 18m
2. Graphs of Equations43m
3. Functions2h 17m
4. Polynomial Functions1h 44m
5. Rational Functions1h 23m
6. Exponential & Logarithmic Functions2h 28m
7. Systems of Equations & Matrices4h 6m
8. Conic Sections2h 23m
9. Sequences, Series, & Induction1h 22m
10. Combinatorics & Probability1h 45m

5. Rational Functions

Asymptotes

College Algebra

5. Rational Functions

Asymptotes

Previous problemNext problem

1:13 minutes

Problem 11

Textbook Question

Use the graph of the rational function in the figure shown to complete each statement in Exercises 9–14.
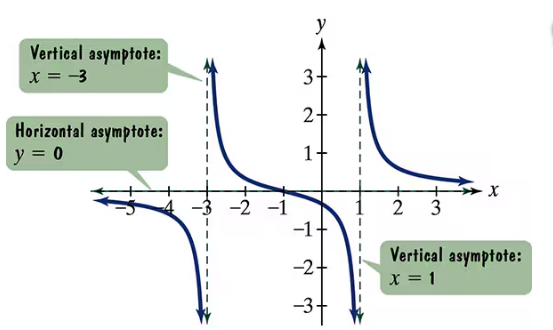
As x -> 1^-, f(x) -> __

Verified step by step guidance

Identify the behavior of the function as x approaches 1 from the left (x -> 1^-).

Observe the graph near x = 1 to determine the direction in which the function is heading.

Notice that as x approaches 1 from the left, the function f(x) is decreasing.

Since the function is decreasing, it is moving towards negative infinity.

Conclude that as x approaches 1 from the left, f(x) approaches negative infinity.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Vertical Asymptotes

Vertical asymptotes occur in rational functions where the function approaches infinity as the input approaches a certain value. In the given graph, vertical asymptotes are present at x = 6 and x = 14, indicating that the function's value becomes unbounded near these x-values. Understanding vertical asymptotes is crucial for analyzing the behavior of rational functions near points of discontinuity.

Horizontal Asymptotes

Horizontal asymptotes describe the behavior of a function as the input approaches infinity or negative infinity. In this graph, the horizontal asymptote is at y = 0, meaning that as x approaches positive or negative infinity, the function's value approaches zero. This concept helps in understanding the long-term behavior of rational functions and their end behavior.

Limits

Limits are fundamental in calculus and algebra, representing the value that a function approaches as the input approaches a certain point. In the context of the question, evaluating the limit of f(x) as x approaches 1 from the left (x -> 1^-) is essential for determining the function's behavior near that point. Understanding limits is key to analyzing continuity and the overall behavior of functions.