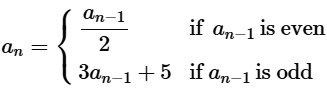
Write the first five terms of the sequence whose first term is 9 and whose general term is an= (an−1)/2 if a_n-1 is even, a_n=3a_n-1 + 5 if a_n-1 is odd for n≥2.

A recursive sequence is defined by a formula that relates each term to one or more previous terms. In this case, the sequence is defined by two rules based on whether the previous term is even or odd. Understanding how to apply these rules is essential for generating the terms of the sequence.

Even numbers are integers divisible by 2, while odd numbers are not. This distinction is crucial in the given problem, as the rules for generating the sequence depend on whether the previous term is even or odd. Recognizing the parity of a number will guide the application of the correct formula for the next term.

Initial conditions are the starting values from which a sequence is generated. In this problem, the first term is given as 9, which is odd. This initial value is critical as it determines the first application of the recursive rules and influences the subsequent terms in the sequence.