Find the slope of each line, provided that it has a slope. 11x + 2y = 3

The slope of a line is a measure of its steepness, typically represented as 'm' in the slope-intercept form of a linear equation, y = mx + b. It is calculated as the ratio of the change in the y-coordinate to the change in the x-coordinate between two points on the line. A positive slope indicates the line rises as it moves from left to right, while a negative slope indicates it falls.

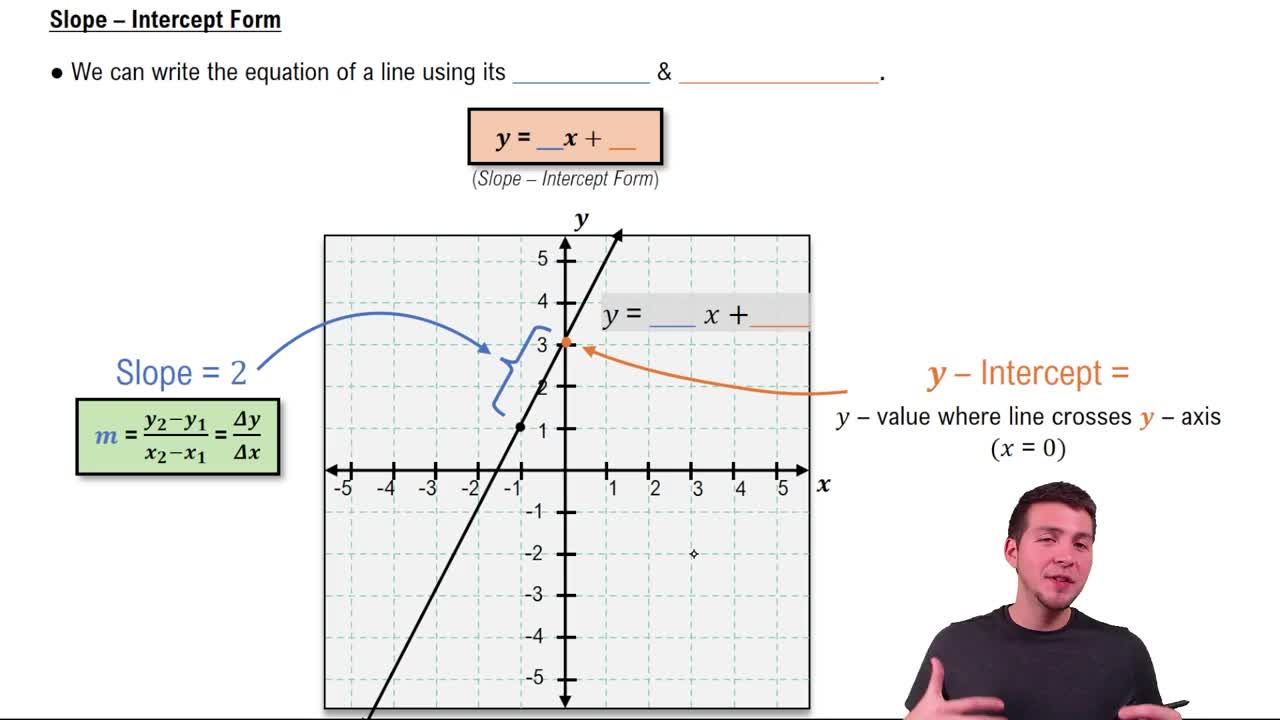
The standard form of a linear equation is expressed as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. This form is useful for identifying the coefficients that can be manipulated to find the slope and y-intercept. To find the slope from this form, one typically rearranges the equation into slope-intercept form.

Rearranging equations involves manipulating the equation to isolate a specific variable, often to convert it into a more useful form, such as slope-intercept form. This process may include adding, subtracting, multiplying, or dividing both sides of the equation by the same value. Understanding how to rearrange equations is essential for solving for variables and interpreting the relationships between them.