Use the intermediate value theorem to show that each polynomial function has a real zero between the numbers given. ƒ(x)=-2x3+5x2+5x-7; 0 and 1
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
Understanding Polynomial Functions
Problem 53
Textbook Question
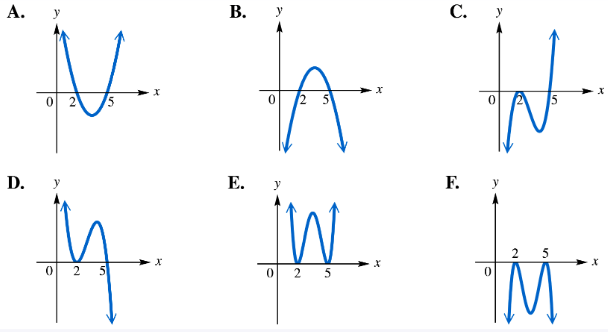
For each polynomial function, identify its graph from choices A–F. ƒ(x)=(x-2)2(x-5)
 Verified step by step guidance
Verified step by step guidance1
Start by identifying the degree of the polynomial function ƒ(x) = (x-2)^2(x-5). Since (x-2)^2 is squared, it contributes degree 2, and (x-5) contributes degree 1, so the total degree is 2 + 1 = 3.
Determine the leading term by multiplying the highest degree terms from each factor: (x)^2 * (x) = x^3. This tells us the polynomial is cubic with a positive leading coefficient, so the end behavior will be: as x → ∞, ƒ(x) → ∞ and as x → -∞, ƒ(x) → -∞.
Identify the zeros of the function from the factors: x = 2 (with multiplicity 2) and x = 5 (with multiplicity 1). The multiplicity affects the graph's behavior at these points.
Analyze the behavior at each zero: at x = 2, since the multiplicity is even (2), the graph will touch the x-axis and turn around (bounce off) at this point; at x = 5, with multiplicity 1 (odd), the graph will cross the x-axis.
Use this information to match the graph: look for a cubic graph that crosses the x-axis at 5, touches and bounces at 2, and has the end behavior of going down to the left and up to the right.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Polynomial Functions and Their Graphs
A polynomial function is an expression involving variables raised to whole-number exponents combined using addition, subtraction, and multiplication. Its graph is a smooth curve with no breaks, and the degree of the polynomial determines the general shape and number of turning points.
Recommended video:

Graphing Polynomial Functions
Zeros and Their Multiplicities
The zeros of a polynomial are the values of x that make the function equal to zero. The multiplicity of a zero indicates how many times that root is repeated, affecting the graph's behavior at that point: even multiplicities cause the graph to touch and turn around, while odd multiplicities cause it to cross the x-axis.
Recommended video:

Finding Zeros & Their Multiplicity
End Behavior of Polynomial Functions
End behavior describes how the graph behaves as x approaches positive or negative infinity. It depends on the leading term's degree and coefficient: for example, an odd-degree polynomial with a positive leading coefficient falls to the left and rises to the right, guiding the overall shape of the graph.
Recommended video:

End Behavior of Polynomial Functions

 6:04m
6:04mWatch next
Master Introduction to Polynomial Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
877
views
