Back
BackProblem 49
In all exercises, other than exercises with no solution, use interval notation to express solution sets and graph each solution set on a number line. In Exercises 27–50, solve each linear inequality. 5(x - 2) - 3(x + 4) ≥ 2x - 20
Problem 51
In Exercises 51–58, solve each compound inequality. 6 < x + 3 < 8
Problem 53
In Exercises 51–58, solve each compound inequality. - 3 ≤ x - 2 < 1
Problem 55
In Exercises 51–58, solve each compound inequality. - 11 < 2x - 1 ≤ - 5
Problem 57
In Exercises 51–58, solve each compound inequality. - 3 ≤ (2/3)x - 5 < - 1
Problem 59
In Exercises 59–94, solve each absolute value inequality. |x| < 3
Problem 61
In Exercises 59–94, solve each absolute value inequality. |x - 1| ≤ 2
Problem 62
In Exercises 59–94, solve each absolute value inequality. |x + 3| ≤ 4
Problem 63
In Exercises 59–94, solve each absolute value inequality. |2x - 6| < 8
Problem 64
In Exercises 59–94, solve each absolute value inequality. |3x + 5| < 17
Problem 65
In Exercises 59–94, solve each absolute value inequality. |2(x - 1) + 4| ≤ 8
Problem 69
In Exercises 59–94, solve each absolute value inequality. |x| > 3
Problem 71
In Exercises 59–94, solve each absolute value inequality. |x - 1| ≥ 2
Problem 73
In Exercises 59–94, solve each absolute value inequality. |3x - 8| > 7
Problem 75
In Exercises 59–94, solve each absolute value inequality. |(2x + 2)/4| ≥ 2
Problem 77
In Exercises 59–94, solve each absolute value inequality. |3 - (2/3)x| > 5
Problem 79
In Exercises 59–94, solve each absolute value inequality. 3|x - 1| + 2 ≥ 8
Problem 81
In Exercises 59–94, solve each absolute value inequality. - 2|x - 4| ≥ - 4
Problem 85
In Exercises 59–94, solve each absolute value inequality. 3 ≤ |2x - 1|
Problem 87
In Exercises 59–94, solve each absolute value inequality. 5 > |4 - x|
Problem 89
In Exercises 59–94, solve each absolute value inequality. 1 < |2 - 3x|
Problem 91
In Exercises 59–94, solve each absolute value inequality.
Problem 95
In Exercises 95–102, use interval notation to represent all values of x satisfying the given conditions.
Problem 100
Use interval notation to represent all values of x satisfying the given conditions. y = |2x - 5| + 1 and y > 9
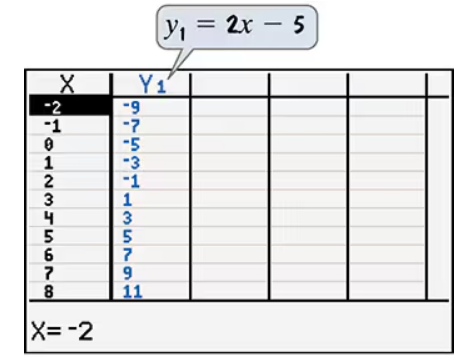
Problem 106
Use the table to solve each inequality. - 3 < 2x - 5 ≤ 3
Problem 107
When 3 times a number is subtracted from 4, the absolute value of the difference is at least 5. Use interval notation to express the set of all numbers that satisfy this condition.
Problem 15
Solve each equation. Then state whether the equation is an identity, a conditional equation, or an inconsistent equation. 2x-5 = 7
Problem 17
Solve each equation. Then state whether the equation is an identity, a conditional equation, or an inconsistent equation. 7(x-4) = x + 2
Problem 19
Solve each equation. Then state whether the equation is an identity, a conditional equation, or an inconsistent equation. 2(x-4)+3(x+5)=2x-2
Problem 22
Solve each equation. Then state whether the equation is an identity, a conditional equation, or an inconsistent equation. 7x + 13 = 2(2x-5) + 3x + 23