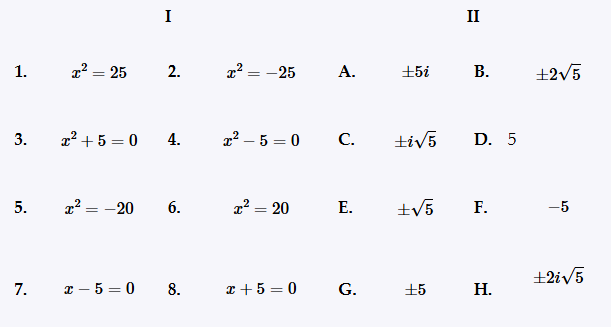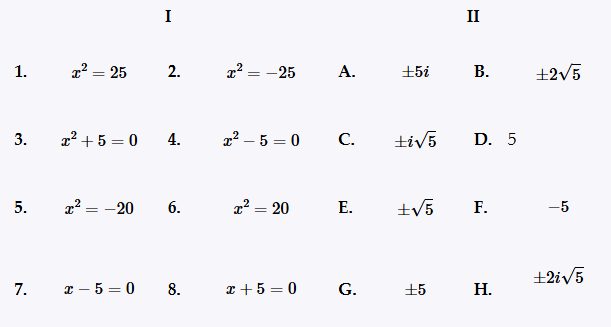Back
BackProblem 65
In the metric system of weights and measures, temperature is measured in degrees Celsius (°C) instead of degrees Fahrenheit (°F). To convert between the two systems, we use the equations. C =5/9 (F-32) and F = 9/5C+32. In each exercise, convert to the other system. Round answers to the nearest tenth of a degree if necessary. 100°F
Problem 67
Work each problem. Round to the nearest tenth of a degree if necessary. Temperature of VenusVenus is the hottest planet, with a surface temperature of 867°F. What is this temperature in degrees Celsius? (Data from The World Almanac and Book of Facts.)
Problem 69
Work each problem. Round to the nearest tenth of a degree if necessary. Temperature in South Carolina A record high temperature of 113°F was recorded for the state of South Carolina on June 29, 2012. What is the corresponding Celsius temperature? (Data from U.S. National Oceanic and Atmospheric Administration.)
Problem 1
Solve each problem. How long will it take a car to travel 400 mi at an average rate of 50 mph?
Problem 2
Solve each problem. If a train travels at 80 mph for 15 min, what is the distance traveled?
Problem 3
Solve each problem. If a person invests $500 at 2% simple interest for 4 yr, how much interest is earned?
Problem 5
Solve each problem. If 120 L of an acid solution is 75% acid, how much pure acid is there in the mixture?
Problem 7
Solve each problem. Suppose two acid solutions are mixed. One is 26% acid and the other is 34% acid. Which one of the following concentrations cannot possibly be the concentration of the mixture? A. 24% B. 30% C. 31% D. 33%
Problem 10
Solve each problem. Which one or more of the following cannot be a correct equation to solve a geometry problem, if x represents the length of a rectangle? (Hint: Solve each equation and consider the solution.) A. 2x+2(x- 1) = 14 B. -2x+7(5-x) = 52 C. 5(x+2)+5x = 10 D. 2x+2(x-3) = 22
Problem 12
Solve each problem. See Example 1. Michael must build a rectangular storage shed. He wants the length to be 6 ft greater than the width, and the perimeter will be 44 ft. Find the length and the width of the shed.
Problem 14
Solve each problem. See Example 1. The length of a rectangular label is 2.5 cm less than twice the width. The perimeter is 40.6 cm. Find the width.
Problem 15
Solve each problem. See Example 1. The perimeter of a triangular plot of land is 2400 ft.The longest side is 200 ft less than twice the shortest. The middle side is 200 ft less than the longest side. Find the lengths of the three sides of the triangular plot.
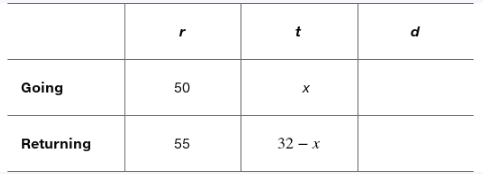
Problem 20
Solve each problem. See Example 2. Elwyn averaged 50 mph traveling from Denver to Minneapolis. Returning by a different route that covered the same number of miles, he averaged 55 mph. What is the distance between the two cities to the nearest ten miles if his total traveling time was 32 hr?
Problem 22
Solve each problem. See Example 2. Two planes leave Los Angeles at the same time. One heads south to San Diego, while the other heads north to San Francisco. The San Diego plane flies 50 mph slower than the San Francisco plane. In 1/2 hr, the planes are 275 mi apart. What are their speeds?
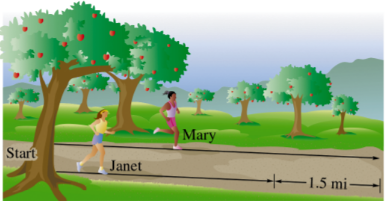
Problem 23
Solve each problem. See Example 2. In the Apple Hill Fun Run, Mary runs at 7 mph, Janet at 5 mph. If they start at the same time, how long will it be before they are 1.5 mi apart?
Problem 25
Solve each problem. See Example 2. At the 2008 Summer Olympics in Beijing, Usain Bolt set a new Olympic and world record in the 100-m dash with a time of 9.69 sec. If this pace could be maintained for an entire 26-mi marathon, what would his time be? How would this time compare to the fastest time for a marathon, which is 2 hr, 3 min, 23 sec, set in 2013? (Hint: 1 m ≈ 3.281 ft.) (Data from Sports Illustrated Almanac.)
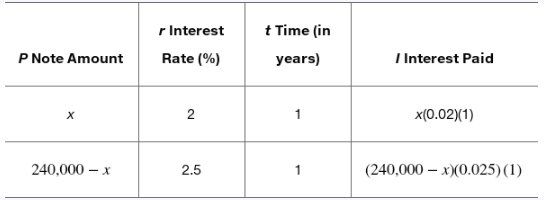
Problem 27
Solve each problem. See Example 2. Callie took 20 min to drive her boat upstream to water-ski at her favorite spot. Coming back later in the day, at the same boat speed, took her 15 min. If the current in that part of the river is 5 km per hr, what was her boat speed?
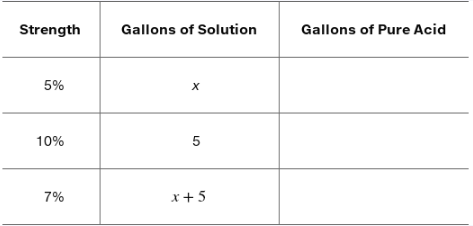
Problem 29
Solve each problem. See Example 3. How many gallons of a 5% acid solution must be mixed with 5 gal of a 10% solution to obtain a 7% solution?
Problem 31
Solve each problem. See Example 3. Aryan wishes to strengthen a mixture from 10% alcohol to 30% alcohol. How much pure alcohol should be added to 7 L of the 10% mixture?
Problem 33
Solve each problem. See Example 3. How much water should be added to 8 mL of 6% saline solution to reduce the concentration to 4%?
Problem 35
Solve each problem. See Example 4. Cody sells some property for $240,000. The money will be paid off in two ways: a short-term note at 2% interest and a long-term note at 2.5%. Find the amount of each note if the total annual interest paid is $5500.
Problem 37
Solve each problem. See Example 4. In planning her retirement, Kaya deposits some money at 2.5% interest, and twice as much money at 3%. Find the amount deposited at each rate if the total annual interest income is $850.
Problem 39
Solve each problem. See Example 4. Zhu inherited $200,000 from her grandmother. She first gave 30% to her favorite charity. She invested some of the rest at 1.5% and some at 4%, earning $4350 interest per year. How much did she invest at each rate?
Problem 43a
Solve each problem. See Examples 5 and 6. Formaldehyde is an indoor air pollutant formerly found in plywood, foam insulation, and carpeting. When concentrations in the air reach 33 micrograms per cubic foot (μg/ft3), eye irritation can occur. One square foot of new plywood could emit 140 μg per hr. (Data from A. Hines, Indoor Air Quality & Control.) A room has 100 ft2 of new plywood flooring. Find a linear equation F that computes the amount of formaldehyde, in micrograms, emitted in x hours.