Systems of Linear Inequalities: Videos & Practice Problems

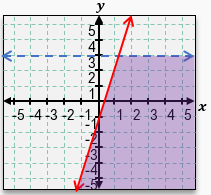
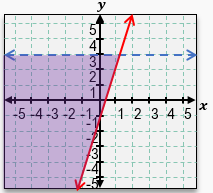
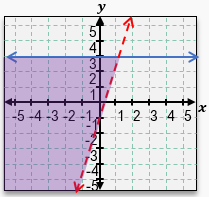
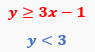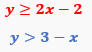Graphing a system of inequalities involves combining the concepts of graphing individual linear inequalities and identifying their overlapping solution regions. Unlike systems of linear equations, which can be solved algebraically, systems of inequalities are typically solved by graphing each inequality and shading the appropriate regions to find where all conditions are simultaneously satisfied.

To graph each inequality, start by converting the inequality into an equation by replacing the inequality symbol with an equal sign. This allows you to graph the boundary line. For example, the inequality \(y \leq -x + 4\) corresponds to the line \(y = -x + 4\), which has a y-intercept of 4 and a slope of -1. The line is drawn solid if the inequality includes equality (≤ or ≥), and dashed if it does not (< or >).

Next, determine which side of the boundary line to shade. This is done by selecting a test point not on the line, commonly the origin \((0,0)\) if it is not on the line, and substituting its coordinates into the inequality. If the inequality holds true for the test point, shade the side of the line containing that point; if false, shade the opposite side. For instance, testing \((0,0)\) in \(y \leq -x + 4\) yields \$0 \leq 4\(, which is true, so shade the side including \)(0,0)\(.

Repeat this process for each inequality in the system. For example, for \)y > 2x + 1\(, graph the dashed line \)y = 2x + 1\( (since the inequality is strict), then test \)(0,0)\(: \)0 > 1\( is false, so shade the side opposite to \)(0,0)$, which is above the line.

The solution to the system of inequalities is the region where the shaded areas overlap. This overlapping region represents all points that satisfy every inequality simultaneously. If no such region exists, the system has no solution.

By carefully graphing each boundary line and shading the correct regions, you can visually identify the solution set to any system of linear inequalities. This method reinforces understanding of linear functions, inequalities, and the geometric interpretation of their solutions.

When graphing a system of linear inequalities, the process involves plotting each inequality as a boundary line and then shading the region that satisfies the inequality. In systems with three inequalities, the approach remains consistent: graph each line, determine the shading direction, and identify the overlapping region that satisfies all inequalities simultaneously. If no such overlap exists, the system has no solution.

Consider the inequality x − y ≥ 2. To graph this, first rewrite it in a more familiar form by isolating y. By rearranging, it becomes y ≤ x − 2. This resembles the slope-intercept form y = mx + b, where the slope m is 1 and the y-intercept b is −2. Graphing the line y = x − 2 involves plotting the y-intercept at (0, −2) and using the slope to find additional points (rise over run = 1). Since the inequality is "less than or equal to," the boundary line is solid, and the shading is below the line, representing all points where y is less than or equal to x − 2.

The second inequality, y ≥ 1, represents a horizontal line crossing the y-axis at 1. Because of the "greater than or equal to" sign, the line is solid, and the shading is above this line, including all points where y is at least 1.

The third inequality, x < 0, corresponds to a vertical line at x = 0. This line is dashed because the inequality is strict ("less than" rather than "less than or equal to"). The shading is to the left of this vertical line, covering all points where x is less than zero.

After graphing all three inequalities with their respective shading, the solution to the system is the region where all shaded areas overlap. If no such common region exists, the system has no solution. In this case, the shaded regions for each inequality do not intersect simultaneously, indicating that there is no solution that satisfies all three inequalities at once.

This method highlights the importance of understanding how to convert inequalities into graphable forms, interpret the meaning of solid versus dashed boundary lines, and apply shading rules based on inequality signs. Mastery of these concepts enables accurate graphing of linear inequalities and identification of solution sets in multi-inequality systems.