A man is dragging a trunk up the loading ramp of a mover's truck. The ramp has a slope angle of $20.0$°, and the man pulls upward with a force $\overrightarrow{F}$ whose direction makes an angle of $30.0$° with the ramp (Fig. E$4.4$). How large will the component $F_y$ perpendicular to the ramp be then?
<IMAGE>

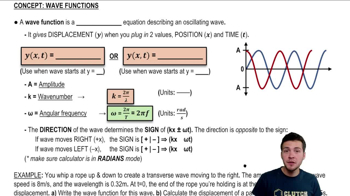
Due to a jaw injury, a patient must wear a strap (Fig. E$4.3$) that produces a net upward force of $5.00$ N on his chin. The tension is the same throughout the strap. To what tension must the strap be adjusted to provide the necessary upward force?

<IMAGE>

To extricate an SUV stuck in the mud, workmen use three horizontal ropes, producing the force vectors shown in Fig. E$4.2$. Use the components to find the magnitude and direction of the resultant of the three pulls.

To extricate an SUV stuck in the mud, workmen use three horizontal ropes, producing the force vectors shown in Fig. E$4.2$. Find the $x$- and $y$-components of each of the three pulls.

Two dogs pull horizontally on ropes attached to a post; the angle between the ropes is $60.0$°. If Rover exerts a force of $270$ N and Fido exerts a force of $300$ N, find the magnitude of the resultant force and the angle it makes with Rover's rope.

A man is dragging a trunk up the loading ramp of a mover's truck. The ramp has a slope angle of $20.0$°, and the man pulls upward with a force $\overrightarrow{F}$ whose direction makes an angle of $30.0$° with the ramp (Fig. E$4.4$). How large a force $\overrightarrow{F}$ is necessary for the component $F_x$ parallel to the ramp to be $90.0$ N?

<IMAGE>

II) Using focused laser light, optical tweezers can apply a force of about 10 pN (piconewtons) to a 1.0-μm-diameter polystyrene bead, which has a density about equal to that of water: a volume of 1.0 cm³ has a mass of about 1.0 g. Estimate the bead's acceleration in g's.

(II) A high-speed 14-car Italian train has a mass of 640 metric tons (640,000 kg). It can exert a maximum force of 400 kN horizontally against the tracks, whereas at maximum constant velocity (300 km/h), it exerts a force of about 150 kN. Calculate a) its maximum acceleration, and (b) estimate the total force of friction and air resistance at top speed.

Superman must stop a 120-km/h train in 150 m to keep it from hitting a stalled car on the tracks. If the train's mass is 3.6 x 10⁵ kg, how much force must he exert? Compare to the weight of the train (give as %). How much force does the train exert on Superman?