Finding the Best Model
In Exercises 5–16, construct a sc...

Question

Finding the Best Model

In Exercises 5–16, construct a scatterplot and identify the mathematical model that best fits the given data. Assume that the model is to be used only for the scope of the given data, and consider only linear, quadratic, logarithmic, exponential, and power models.

Stock Market Listed below in order by row are the annual high values of the Dow Jones Industrial Average for each year beginning with 2000. Find the best model and then predict the value for the last year listed. Is the predicted value close to the actual value of 26,828.4?

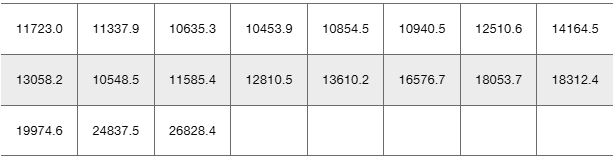
Table showing annual high values of the Dow Jones Industrial Average from 2000, used for model fitting and prediction.

Accepted Answer

Hello. In this video, we are told that the following data lists the revenue from a startup, from a tech startup over several years. We want to construct a scatter plot to determine the best mathematical model for the data set. So in this problem we are going to be using Google Sheets to help us solve or create the model that best fits the data set. Now what we want to go ahead and do in this case is we want to take this given data set and separate it into two columns in our program. So let's go ahead and switch over to Google Sheets. So what I have here is the data set that was given to us. We have one column that represents the different years and one column that represents the different revenue. Now, in order to create the model that best fits the data set, the first thing you want to do is you want to select the entire data set. Then what we want to go ahead and do is we want to go ahead and insert a chart. Now, once we get this chart, we want to go ahead and go to our setup. Where we see line chart, we want to scroll down until we find a scatter plot, because we want to be working with a scatter plot for the different data points. So this is how our new chart is going to look. Now, what we want to go ahead and do in order to find the best fitting model, is we're going to click on one of the points. And what we're going to do is we're going to activate or select our trend line, and what the trend line does is it's going to give us an option for the different models that we can represent the data set with. So we have some different options. We have linear, exponential, polynomial, logarithmic, power, and moving average. But we wanna go ahead and keep with respect to linear exponential polynomial logarithmic. So we're gonna scroll through each of the options and pick which one best fits the data set that is given to us. Now, if we're looking at linear, a lot of the points deviate away from the line, so linear is not a best fit. Exponential is a little bit better, but we still see that some of the points get disaligned from the exponential graph, so this won't be our pick. Logarithmic has the same problem as the linear as many of the points scatter away from the trend line. And if we take a look at polynomial, polynomial fits fairly well. Now, when you select polynomial, one thing to note is that you definitely want to make sure that you have a polynomial of degree 2, so you have an accurate coefficient of determination. So, as we can see, the trend line for polynomial is going to best fit the data set. So that means that the polynomial option is going to be the best model for the data set that is given to us. And polynomial again was underneath the quadratic option. So going back to the problem, the correct solution for this is going to be option B. So I hope this video helps you in understanding how to approach this problem, and we will go ahead and see you all in the next video.

Key Concepts

Scatterplot Construction

Model Selection and Types

Prediction and Model Validation

Watch next