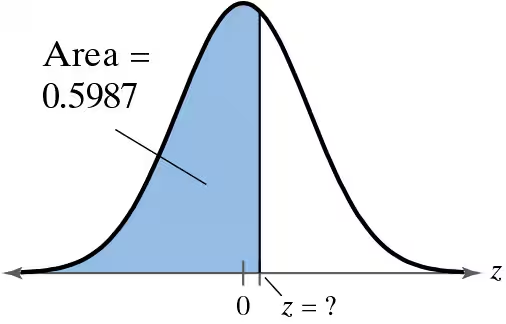
Finding Probability In Exercises 47–56, find the indicated probability using the standard normal distribution. If convenient, use technology to find the probability.
P(z < - 1.11)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 7:09m
7:09mMaster Probability From Given Z-Scores - TI-84 (CE) Calculator with a bite sized video explanation from Patrick
Start learning