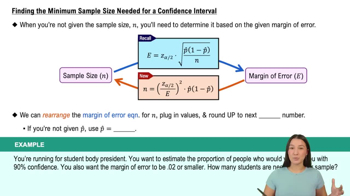
Congress You wish to estimate, with 95% confidence, the population proportion of likely U.S. voters who think Congress is doing a good or excellent job. Your estimate must be accurate within 4% of the population proportion.
b. Find the minimum sample size needed, using a prior survey that found that 21% of likely U.S. voters think Congress is doing a good or excellent job. (Source: Rasmussen Reports)