In a recent year, according to the Bureau of Labor Statistics,...

Question

In a recent year, according to the Bureau of Labor Statistics, the median number of years that wage and salary employees had been with their current employer (called employee tenure) was 4.1 years. Information on employee tenure has been gathered since 1996 using the Current Population Survey (CPS), a monthly survey of about 60,000 households that provides information on employment, unemployment, earnings, demographics, and other characteristics of the U.S. population ages 16 and over. With respect to employee tenure, the questions measure how long employees have been with their current employers, not how long they plan to stay with their employers.

A congressional representative claims that the median tenure for employees from the representative’s district is less than the national median tenure of 4.1 years. The claim is based on the representative’s data, which is shown in the table at the right above. (Assume that the employees were randomly selected.)

c. State the null hypothesis and the alternative hypothesis.

A congressional representative claims that the median tenure for employees from the representative’s district is less than the national median tenure of 4.1 years. The claim is based on the representative’s data, which is shown in the table at the right above. (Assume that the employees were randomly selected.)

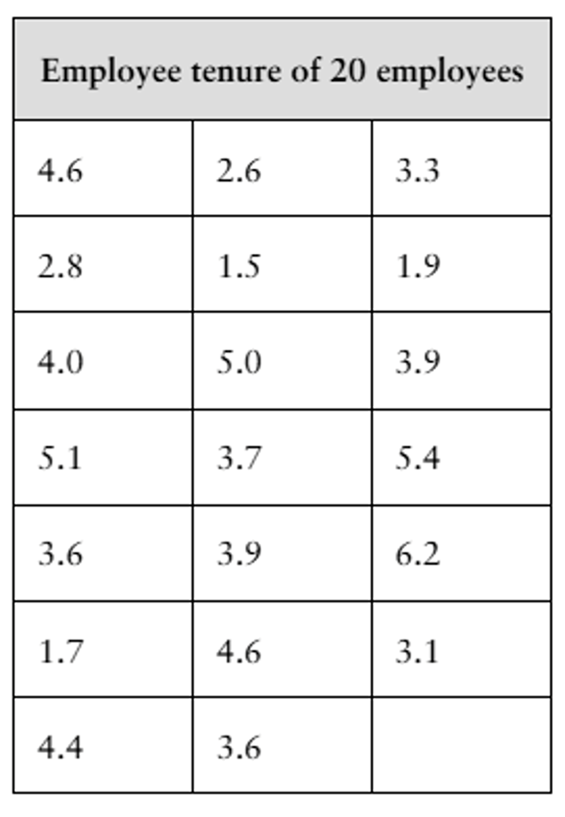
Table displaying employee tenure data for 20 individuals, with values ranging from 1.5 to 6.2 years.

a. Is it possible that the claim is true? What questions should you ask about how the data were collected?

Accepted Answer

Hello there. Today we're gonna solve the following practice problem together. So, first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. A university administrator claims that the median number of years that faculty have worked at the university is less than the national median of 7.8 years, based on a survey of the faculty at the university. The national median comes from a comprehensive higher education report. Is it possible that the administrator's claim is valid? What questions should you ask about the survey? Awesome. So it appears for this particular problem we're asked to solve for two separate answers. We're asked to determine whether or not it is considered possible that the administrator's claim is valid, noting that the claim once again is, is that the median number of years that faculty have worked at the university is less than the national median, which is 7.8 years. And once we've determined whether or not it's possible that the administrator's claim is valid, that's our first answer we're trying to solve for. Our second answer we're trying to solve for is we're trying to ask what questions are needed to be asked about this survey. So what questions should we ask about this particular survey? That's our second answer that we're ultimately trying to solve for. So now that we know what we're trying to solve for, our first step that we need to take in order to solve for this particular problem, as we should recall, we need to compare the university survey median to the national median of 7.8 years. That's our first step, so we're asked to compare. Our second step, as we should recall, is we need to ask if the sample of the faculty members was randomly selected and that it represents all of the faculty at the university. Our 3rd step, as we should recall, is we need to ask about the sample size and whether it is sufficient for reliable conclusions. Our fourth step is we, as we should recall, is we need to ask if there were any biases in the data collection, because we have to always look out for bias, such as only including certain departments or ranks, so we need to determine whether or not any bias is present at any part or any. Area of this particular survey. Moving right along here, our 5th step is we need to confirm that the definition of years worked matches the national report's definition of years worked, so they have to be the same. And our 6th step we need to check if the timing of the data collection matches the national report period. And finally, our 7th and final step is we need to make our final conclusions, which we need to conclude based on what we've gone over together, that the claim could be true. But more information about the data collection and sample representativeness, so how it's being represented is needed. So we need to have more information about how the sample data is represented or represented in the in both studies in order to compare it. So, with that in mind, to summarize what we've learned, our final two answers without a doubt will have to be the following. Yes, the administrator's claim may be valid is our first answer, and our second answer is, we should ask about random sampling, sample size, representativeness, and definition of years worked and survey timing, and that's it. Those are our final two answers. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

Key Concepts

Median

Random Sampling

Hypothesis Testing

Watch next