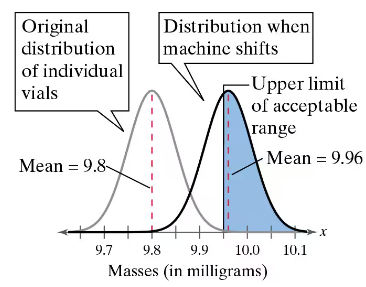
In Exercises 39 and 40, determine whether the finite correction factor should be used. If so, use it in your calculations when you find the probability.
Old Faithful In a sample of 100 eruptions of the Old Faithful geyser at Yellowstone National Park, the mean interval between eruptions was 129.58 minutes and the standard deviation was 108.54 minutes. A random sample of size 30 is selected from this population. What is the probability that the mean interval between eruptions is between 120 minutes and 140 minutes?