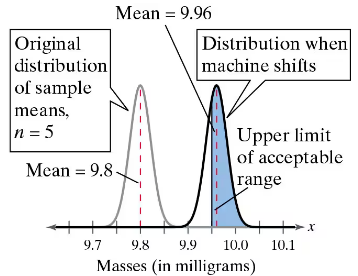
Interpreting the Central Limit Theorem In Exercises 19–26, find the mean and standard deviation of the indicated sampling distribution of sample means. Then sketch a graph of the sampling distribution.
Renewable Energy The zloty is the official currency of Poland. During a recent period of two years, the day-ahead prices for renewable energy in Poland (in zlotys per mega-watt hour) have a mean of 158.51 and a standard deviation of 33.424. Random samples of size 100 are drawn from this population, and the mean of each sample is determined. (Adapted from Multidisciplinary Digital Publishing Institute)