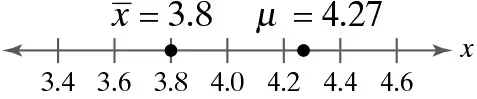Graphical Analysis In Exercises 9–12, use the values on the number line to find the sampling error.

In Exercises 53 and 54, find the mean and standard deviation of the indicated sampling distribution of sample means. Then sketch a graph of the sampling distribution.

The test scores for the Law School Admission Test (LSAT) in a recent year are normally distributed, with a mean of 151.88 and a standard deviation of 9.95. Random samples of size 40 are drawn from this population, and the mean of each sample is determined.

For the same sample statistics, which level of confidence would produce the widest confidence interval? Explain your reasoning.

a. 90%

b. 95%

c. 98%

d. 99%

In Exercises 5–8, find the critical value zc necessary to construct a confidence interval at the level of confidence c.

c = 0.80

In Exercises 5–8, find the critical value zc necessary to construct a confidence interval at the level of confidence c.

c = 0.97

Graphical Analysis In Exercises 9–12, use the values on the number line to find the sampling error.

In Exercises 13–16, find the margin of error for the values of c, σ and n.

c = 0.95, σ = 5.2, n = 30

In Exercises 13–16, find the margin of error for the values of c, σ and n.

c = 0.975, σ = 4.6, n = 100

Matching In Exercises 17–20, match the level of confidence c with the appropriate confidence interval. Assume each confidence interval is constructed for the same sample statistics.

c = 0.88