Hypothesis Testing Using Rejection Regions In Exercises 23–30,...

Question

Hypothesis Testing Using Rejection Regions In Exercises 23–30, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic X^2, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the population is normally distributed.

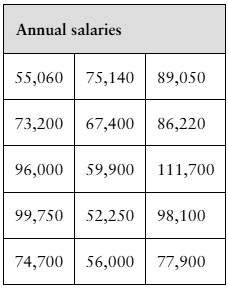
Salaries The annual salaries (in dollars) of 15 randomly chosen senior level graphic design specialists are shown in the table at the left. At α=0.05, is there enough evidence to support the claim that the standard deviation of the annual salaries is different from $13,056?

tab1

Accepted Answer

Hello, everyone. Let's take a look at this question together. The monthly rent in dollars paid by 12 randomly selected residents in the city is listed below, and here we have the data values for the monthly rent in dollars paid by the 12 randomly selected residents. At the alpha equals 0.05 level of significance, is there sufficient evidence to conclude that the standard deviation of monthly rent is different from $25? Assume the population is normally distributed. Is it answer choice? A, there is no sufficient evidence to conclude that the standard deviation of the monthly rent is different from $25. Answer choice B, there is sufficient evidence to conclude that the standard deviation of the monthly rent is different from $25 or answer choice C, not enough information. So, in order to solve this question, we have to recall how we can test this claim that the standard deviation of monthly rent is different from $25 at the alpha equals 0.05 level of significance, given that we have 12 randomly selected residents in a city with the following data values for their monthly rent in. and we assume the population is normally distributed. Well, the first step in testing this claim is identifying the given data, which includes a sample size N equals 12, a claimed standard deviation of 25, a significance level of alpha equals 0.05, the following data values for the monthly paid rent. And that the population is normally distributed. So then using this information, we must identify the claim and state the hypotheses, which the claim is that the population standard deviation is different from $25 so we can identify that this is a two-tailed test. So our null hypothesis is that The population standard deviation is equal to $25 and our alternative hypothesis is that the standard deviation is not equal to $25. Then the next step is to find the standardized test statistic which we will compute the chi square test statistic. Starting with the mean, which is X bar is equal to the sum of all of the X values divided by our sample size N. So plugging in the values from the data into the formula, we have all of the values for the monthly paid rent, divided by 12, which is our sample size, giving us 11,950 divided by 12, so our mean value is equal to 995.83. And then using the mean, we can determine the sum of the squared difference between X values and the mean, which is equal to 5,591.67 and now we can calculate our sample variance, which is equal to the sum of the squared difference between the X values and the mean divided by our sample size and subtracted by 1. So plugging in the values into the sample variance formula, we have 508.30. 3 as the value for the sample variants, and then using that value we can determine our test statistic, which is chi square is equal to in parentheses and minus 1 multiplied by the sample variants divided by the population variances, which plugging in the values into that formula, our test statistic is equal to 8.95. And now we can calculate our critical values. Which for a two-tail test with alpha equals 0.05, and our degrees of freedom, which is calculated as N minus 1, so 12 minus 1 is equal to 11, we know from the chi square distribution tables that our left critical value is approximately 3.816, and our right critical value is approximately 21.920. Therefore, our rejection. The region is that we reject the null hypothesis if the test statistic is less than 3.186 or greater than 21.920. Therefore, we can make our decision, which we know we computed our test statistic is equal to 8.95, which 8.95 is between the critical values, therefore, we fail to reject the null hypothesis. So in conclusion, At the 0.05 significance level, there is no sufficient evidence to conclude that the standard deviation of the monthly rent is different from $25 which, looking at our answer choices, we can identify answer choice A is the correct answer. As we know, there is no sufficient evidence to conclude that the standard deviation of the monthly rent is different from $25. And all other answer choices are incorrect. I hope you found this video to be helpful. Thank you and goodbye.

Key Concepts

Hypothesis Testing

Critical Value and Rejection Region

Standard Deviation and Chi-Square Test

Watch next