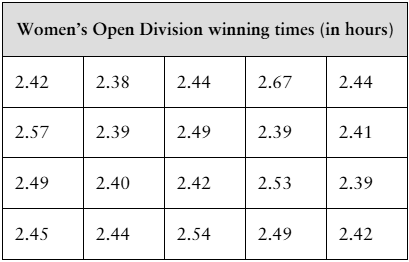
When all other quantities remain the same, how does the indicated change affect the width of a confidence interval? Explain.
c. Increase in the population standard deviation
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:



 4:48m
4:48mMaster Population Standard Deviation Known with a bite sized video explanation from Patrick
Start learning