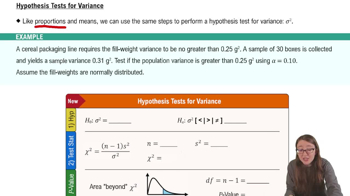
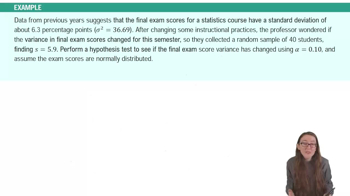
9. Hypothesis Testing for One Sample

A machine produces ball bearings that are designed to have a diameter standard deviation of 0.04 mm, but an engineer suspects the variability has increased. A sample of 60 bearings shows a standard deviation of 0.052 mm. Perform a hypothesis test with $\alpha =0.01$ to test the claim. Should the line manager have the machine serviced?

Testing Claims About Variation

In Exercises 5–16, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Assume that a simple random sample is selected from a normally distributed population.

Pulse Rates of Men A simple random sample of 153 men results in a standard deviation of 11.3 beats per minute (based on Data Set 1 “Body Data” in Appendix B). The normal range of pulse rates of adults is typically given as 60 to 100 beats per minute. If the range rule of thumb is applied to that normal range, the result is a standard deviation of 10 beats per minute. Use the sample results with a 0.05 significance level to test the claim that pulse rates of men have a standard deviation equal to 10 beats per minute; see the accompanying StatCrunch display for this test. What do the results indicate about the effectiveness of using the range rule of thumb with the “normal range” from 60 to 100 beats per minute for estimating in this case?

Testing Claims About Variation

In Exercises 5–16, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Assume that a simple random sample is selected from a normally distributed population.

Minting of Pennies Data Set 40 “Coin Weights” lists weights (grams) of pennies minted after 1983. Here are the statistics for those weights: n = 37, xbar = 2.49910 g, s = 0.01648 g . Use a 0.05 significance level to test the claim that the sample is from a population of pennies with weights having a standard deviation greater than 0.01000 g.

Testing Claims About Variation

In Exercises 5–16, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Assume that a simple random sample is selected from a normally distributed population.

Bank Lines The Jefferson Valley Bank once had a separate customer waiting line at each teller window, but it now has a single waiting line that feeds the teller windows as vacancies occur. The standard deviation of customer waiting times with the old multiple-line configuration was 1.8 min. Listed below is a simple random sample of waiting times (minutes) with the single waiting line. Use a 0.05 significance level to test the claim that with a single waiting line, the waiting times have a standard deviation less than 1.8 min. What improvement occurred when banks changed from multiple waiting lines to a single waiting line?

6.5 6.6 6.7 6.8 7.1 7.3 7.4 7.7 7.7 7.7

Finding Critical Values of (chi)^2 For large numbers of degrees of freedom, we can approximate critical values of as follows:

(chi)^2 = (1/2)(z + sqrt(2k-1))

Here k is the number of degrees of freedom and z is the critical value(s) found from technology or Table A-2. In Exercise 12 “Spoken Words” we have df = 55, so Table A-4 does not list an exact critical value. If we want to approximate a critical value of (chi)^2 in the right-tailed hypothesis test with α = 0.01 and a sample size of 56, we let k =55 with z = 2.33 (or the more accurate value of z = 2.326348 found from technology). Use this approximation to estimate the critical value of for Exercise 12. How close is it to the critical value of (chi)^2 = 82.292 obtained by using Statdisk and Minitab?