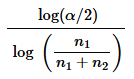In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Do Men Talk Less than Women? Listed below are word counts of males and females in couple relationships (from Data Set 14 “Word Counts” in Appendix B).

a. Use a 0.05 significance level to test the claim that men talk less than women.

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Measured and Reported Weights Listed below are measured and reported weights (lb) of random female subjects (from Data Set 4 “Measured and Reported” in Appendix B).

b. Construct the confidence interval that could be used for the hypothesis test described in part (a). What feature of the confidence interval leads to the same conclusion reached in part (a)?

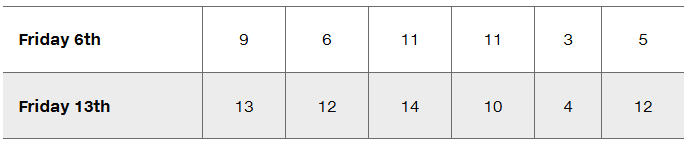
Is Friday the 13th Unlucky? Listed below are numbers of hospital admissions in one region due to traffic accidents on different Fridays falling on the 6th day of a month and the following 13th day of the month (based on data from “Is Friday the 13th Bad for Your Health,” by Scanlon et al., British Medical Journal, Vol. 307). Assume that we want to use a 0.05 significance level to test the claim that the data support the claim that fewer hospital admissions due to traffic accidents occur on Friday the 6th than on the following Friday the 13th. Identify the null hypothesis and alternative hypothesis.

Friday the 13th Refer to the sample data from Exercise 1.

a. Find the differences d, then find the values of d_bar and sd

Friday the 13th Refer to the sample data from Exercise 1.

b. In general, what does ud represent?

Confidence Interval Assume that we want to use the sample data in Exercise 1 for constructing a confidence interval to be used for testing the given claim.

a. What is the confidence level that should be used for the confidence interval?

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Measured and Reported Weights Listed below are measured and reported weights (lb) of random female subjects (from Data Set 4 “Measured and Reported” in Appendix B).

a. Use a 0.05 significance level to test the claim that for females, the measured weights tend to be higher than the reported weights.

In Exercises 5–16, use the listed paired sample data, and assume that the samples are simple random samples and that the differences have a distribution that is approximately normal.

Heights of Presidents A popular theory is that presidential candidates have an advantage if they are taller than their main opponents. Listed are heights (cm) of presidents along with the heights of their main opponents (from Data Set 22 “Presidents” in Appendix B).

b. Construct the confidence interval that could be used for the hypothesis test described in part (a). What feature of the confidence interval leads to the same conclusion reached in part (a)?

In Exercises 17–24, use the indicated Data Sets from Appendix B. The complete data sets can be found at www.TriolaStats.com. Assume that the paired sample data are simple random samples and the differences have a distribution that is approximately normal.

Measured and Reported Weights Repeat Example 1 using all of the 2784 measured and reported weights of males listed in Data Set 4 “Measured and Reported” in Appendix B. Did the larger data set have much of an effect on the results?

F Test Statistic

a. If s2,1 represents the larger of two sample variances, can the F test statistic ever be less than 1?

F Test Statistic

b. Can the F test statistic ever be a negative number?

F Test Statistic

c. If testing the claim that sigma2,1 is not equals to sigma2,2 what do we know about the two samples if the test statistic F is very close to 1?

F Test Statistic

d. Is the F distribution symmetric, skewed left, or skewed right?

Color and Creativity Researchers from the University of British Columbia conducted trials to investigate the effects of color on creativity. Subjects with a red background were asked to think of creative uses for a brick; other subjects with a blue background were given the same task. Responses were scored by a panel of judges and results from scores of creativity are given below. Use a 0.05 significance level to test the claim that creative task scores have the same variation with a red background and a blue background.

[Image]

Second-Hand Smoke Samples from Data Set 15 “Passive and Active Smoke” include cotinine levels measured in a group of smokers ( n = 40, x_bar = 172.48 ng/mL, 119.50 ng/mL ) and a group of nonsmokers not exposed to tobacco smoke ( n = 40, x_bar = 16.35 ng/mL, 62.53 ng/mL ). Cotinine is a metabolite of nicotine, meaning that when nicotine is absorbed by the body, cotinine is produced.

a. Use a 0.05 significance level to test the claim that the variation of cotinine in smokers is greater than the variation of cotinine in nonsmokers not exposed to tobacco smoke.

Second-Hand Smoke Samples from Data Set 15 “Passive and Active Smoke” include cotinine levels measured in a group of smokers ( n = 40, x_bar = 172.48 ng/mL, 119.50 ng/mL ) and a group of nonsmokers not exposed to tobacco smoke ( n = 40, x_bar = 16.35 ng/mL, 62.53 ng/mL ). Cotinine is a metabolite of nicotine, meaning that when nicotine is absorbed by the body, cotinine is produced.

b. The 40 cotinine measurements from the nonsmoking group consist of these values (all in ng/mL): 1, 1, 90, 244, 309, and 35 other values that are all 0. Does this sample appear to be from a normally distributed population? If not, how are the results from part (a) affected?

Test for Normality For the hypothesis test described in Exercise 2, the sample sizes are n1 = 2208 and n2 = 1986 When using the F test with these data, is it correct to reason that there is no need to check for normality because both samples have sizes that are greater than 30?

Robust What does it mean when we say that the F test described in this section is not robust against departures from normality?

Count Five Test for Comparing Variation in Two Populations Repeat Exercise 16 “Blanking Out on Tests,” but instead of using the F test, use the following procedure for the “count five” test of equal variations (which is not as complicated as it might appear).

a. For each value x in the first sample, find the absolute deviation |x-x_bar| then sort the absolute deviation values. Do the same for the second sample.

Count Five Test for Comparing Variation in Two Populations Repeat Exercise 16 “Blanking Out on Tests,” but instead of using the F test, use the following procedure for the “count five” test of equal variations (which is not as complicated as it might appear).

b. Let c1 be the count of the number of absolute deviation values in the first sample that are greater than the largest absolute deviation value in the other sample. Also, let C2 be the count of the number of absolute deviation values in the second sample that are greater than the largest absolute deviation value in the other sample. (One of these counts will always be zero.)

Count Five Test for Comparing Variation in Two Populations Repeat Exercise 16 “Blanking Out on Tests,” but instead of using the F test, use the following procedure for the “count five” test of equal variations (which is not as complicated as it might appear).

c. If the sample sizes are equal (n1 = n2) use a critical value of 5. If n1 is not equals to n2 calculate the critical value shown below.

Count Five Test for Comparing Variation in Two Populations Repeat Exercise 16 “Blanking Out on Tests,” but instead of using the F test, use the following procedure for the “count five” test of equal variations (which is not as complicated as it might appear).

d. If c1 equal to or greater than critical value then conclude that sigma2,1 > sigma2,2 If c1 equal to or greater than critical value then conclude that sigma2,2 > sigma2,1. Otherwise, fail to reject the null hypothesis of sigma2,1 = sigma2,2

Bootstrapping and Randomization When resampling data from two independent samples, what is the fundamental difference between bootstrapping and randomization?

Sampling Methods A student obtains a sample of responses to the question “Do you plan to take or have you taken a statistics course?” A second student obtains a sample of responses to the same question. The first student surveys only males at the same college, and the second student surveys only females at the same college. What is wrong with the samples? Can randomization be used to overcome the flaws of those samples?

Randomization vs t Test Two samples of commute times from Boston and New York are randomly selected and it is found that the samples sizes are n1 = 18 and n2 = 12 and each of the two samples appears to be from a population with a distribution that is dramatically far from normal. Which method is more likely to yield better results for testing Mu1 is not equals to Mu2. Hypothesis test using the t distribution (as in Section 9-2) or the resampling method?

In Exercises 5–8, use (a) randomization and (b) bootstrapping for the indicated exercise from Section 9-1. Compare the results to those obtained in the original exercise.

Exercise 7 in Section 9-1 “Buttered Toast Drop”

In Exercises 5–8, use (a) randomization and (b) bootstrapping for the indicated exercise from Section 9-1. Compare the results to those obtained in the original exercise.

Exercise 8 in Section 9-1 “Tennis Challenges”

In Exercises 5–8, use (a) randomization and (b) bootstrapping for the indicated exercise from Section 9-1. Compare the results to those obtained in the original exercise.

Exercise 9 in Section 9-1 “Cell Phones and Handedness”

Body Temperatures Listed below are body temperatures from six different subjects measured at two different times in a day (from Data Set 5 “Body Temperatures” in Appendix B).

a. Are the two sets of data independent or dependent? Explain.

[Image]

Denomination Effect A trial was conducted with 75 women in China given a 100-yuan bill, while another 75 women in China were given 100 yuan in the form of smaller bills (a 50-yuan bill plus two 20-yuan bills plus two 5-yuan bills). Among those given the single bill, 60 spent some or all of the money. Among those given the smaller bills, 68 spent some or all of the money (based on data from “The Denomination Effect,” by Raghubir and Srivastava, Journal of Consumer Research, Vol. 36). We want to use a 0.05 significance level to test the claim that when given a single large bill, a smaller proportion of women in China spend some or all of the money when compared to the proportion of women in China given the same amount in smaller bills.

a. Test the claim using a hypothesis test.