Textbook Question
Determine the largest open intervals of the domain over which each function is (c) constant. See Example 8.
389
views
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: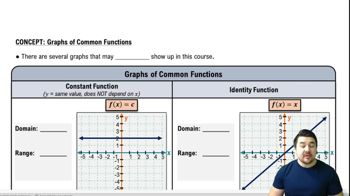



 5:2m
5:2mMaster Introduction to Relations and Functions with a bite sized video explanation from Patrick
Start learning