Textbook Question
Determine whether each relation defines y as a function of x. Give the domain and range. See Example 5.y = x²
434
views
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: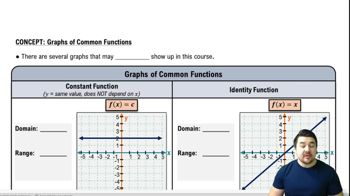



 5:2m
5:2mMaster Introduction to Relations and Functions with a bite sized video explanation from Patrick
Start learning