Find the linear speed v for each of the following.
a point on the edge of a flywheel of radius 2 m, rotating 42 times per min
 Verified step by step guidance
Verified step by step guidance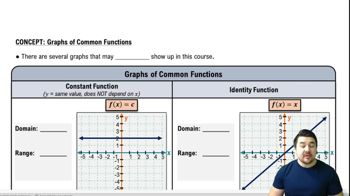



 6:11m
6:11mMaster Introduction to the Unit Circle with a bite sized video explanation from Patrick
Start learning