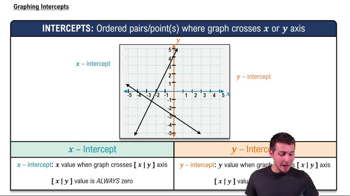
A rotating beacon is located at point A, 4 m from a wall. The distance a is given by
a = 4 |sec 2πt|,
where t is time in seconds since the beacon started rotating. Find the value of a for each time t. Round to the nearest tenth if applicable.
<IMAGE>
t = 1.24