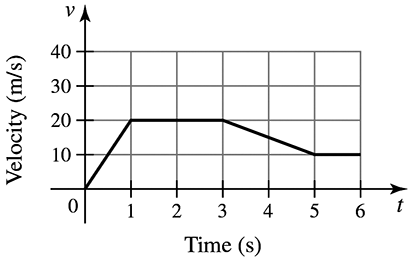
Explain why or why not Determine whether the following statements are true and give an explanation or counterexample. Assume ƒ and ƒ' are continuous functions for all real numbers.
(d) If ƒ is continuous on [a,b] and ∫ₐᵇ |ƒ(𝓍)| d𝓍 = 0 , then ƒ(𝓍) = 0 on [a,b] .