Evaluate the integral by interpreting it in terms of areas: .
Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
- 12. Techniques of Integration7h 39m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
8. Definite Integrals
Estimating Area with Finite Sums
Problem 5.1.71c
Textbook Question
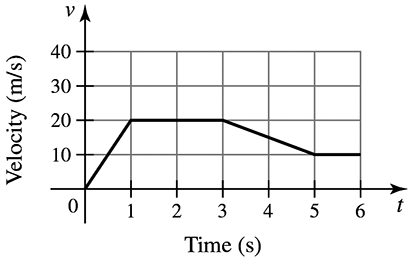
Displacement from a velocity graph Consider the velocity function for an object moving along a line (see figure).
(c) Use geometry to find the displacement of the object between t = 2 and t = 5.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the problem. The displacement of the object between t = 2 and t = 5 can be found by calculating the area under the velocity graph between these time intervals. The graph consists of geometric shapes (rectangles and triangles) that can be used to compute the area.
Step 2: Identify the shapes under the graph between t = 2 and t = 5. From t = 2 to t = 3, the graph forms a rectangle. From t = 3 to t = 5, the graph forms a triangle.
Step 3: Calculate the area of the rectangle from t = 2 to t = 3. The height of the rectangle is the velocity at t = 2, which is 20 m/s, and the width is the time interval, which is 1 second. Use the formula for the area of a rectangle: .
Step 4: Calculate the area of the triangle from t = 3 to t = 5. The base of the triangle is the time interval, which is 2 seconds, and the height is the change in velocity, which is 20 m/s - 10 m/s = 10 m/s. Use the formula for the area of a triangle: .
Step 5: Add the areas of the rectangle and triangle to find the total displacement of the object between t = 2 and t = 5. The sum of these areas represents the total displacement in meters.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Velocity Function
The velocity function describes how the velocity of an object changes over time. It is a graphical representation where the y-axis represents velocity (in meters per second) and the x-axis represents time (in seconds). Understanding this function is crucial for analyzing the motion of the object, as it provides insights into how fast and in what direction the object is moving at any given moment.
Recommended video:

Using The Velocity Function
Displacement
Displacement is the overall change in position of an object over a specific time interval. It can be calculated by finding the area under the velocity graph between two time points. In this case, the displacement from t = 2 to t = 5 seconds can be determined by calculating the area of the geometric shapes formed by the velocity graph within that interval, which represents the total distance traveled in that time frame.
Recommended video:

Using The Velocity Function
Area Under the Curve
In calculus, the area under a curve on a graph represents the integral of a function over a specified interval. For a velocity graph, this area corresponds to the displacement of the object. By using geometric shapes such as rectangles and triangles, one can calculate the area under the curve between two time points, which provides the total displacement of the object during that time period.
Recommended video:

Estimating the Area Under a Curve with Right Endpoints & Midpoint

 7:59m
7:59mWatch next
Master Estimating the Area Under a Curve Using Left Endpoints with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
4
views
