50-53. Reduction Formulas Use integration by parts to derive the following reduction formulas:
53. ∫ lnⁿ(x) dx = x lnⁿ(x) - n ∫ lnⁿ⁻¹(x) dx
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: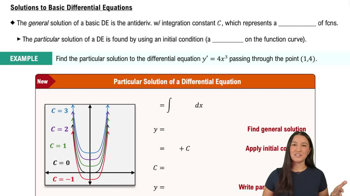
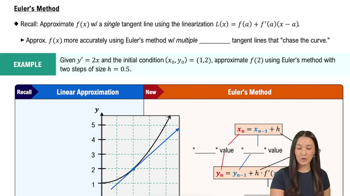
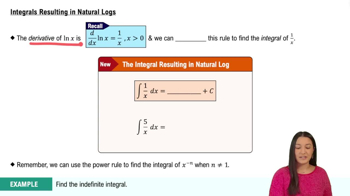

 8:30m
8:30mMaster Introduction to Integration by Parts with a bite sized video explanation from Patrick
Start learning