For each function graphed, give the minimum and maximum values of ƒ(x) and the x-values at which they occur.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
3. Functions
Intro to Functions & Their Graphs
Problem 7
Textbook Question
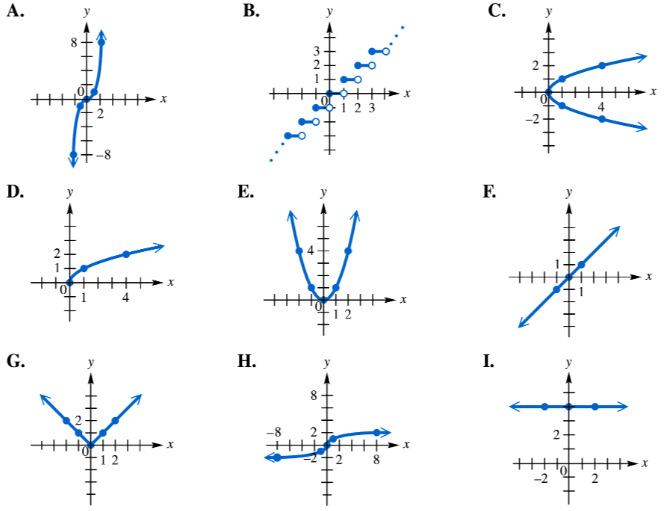
To answer each question, refer to the following basic graphs. Which one is the graph of ƒ(x)=∛x? Is there any open interval over which the function is decreasing?
 Verified step by step guidance
Verified step by step guidance1
Recall that the function \( f(x) = \sqrt[3]{x} \) is the cube root function, which is defined for all real numbers \( x \). Its graph passes through the origin \( (0,0) \) and has a characteristic S-shape, increasing from left to right.
Identify the graph of \( f(x) = \sqrt[3]{x} \) by looking for the curve that is continuous for all \( x \), passes through the origin, and increases slowly for negative \( x \) values (going down to the left) and increases for positive \( x \) values (going up to the right).
To determine if the function is decreasing on any open interval, consider the derivative of \( f(x) = \sqrt[3]{x} \). The derivative is \( f'(x) = \frac{1}{3x^{2/3}} \), which is positive for all \( x \neq 0 \).
Since \( f'(x) > 0 \) for all \( x \neq 0 \), the function is strictly increasing everywhere except possibly at \( x = 0 \), where the derivative is undefined but the function is still increasing through that point.
Therefore, there is no open interval over which \( f(x) = \sqrt[3]{x} \) is decreasing; it is increasing on its entire domain.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Cube Root Function
The cube root function, denoted as ƒ(x) = ∛x, returns the number that, when cubed, equals x. Its graph is symmetric about the origin and passes through (0,0). Unlike square roots, it is defined for all real numbers, including negatives.
Recommended video:

Imaginary Roots with the Square Root Property
Graph Interpretation
Understanding how to read and interpret graphs is essential. This includes recognizing key features such as intercepts, symmetry, and the general shape of the curve, which helps identify the function represented by the graph.
Recommended video:
Guided course

Graphs and Coordinates - Example
Increasing and Decreasing Intervals
A function is increasing on an interval if its output values rise as x increases, and decreasing if outputs fall. Determining these intervals involves analyzing the slope or derivative of the function or observing the graph's behavior over specific intervals.
Recommended video:

Identifying Intervals of Unknown Behavior

 5:2m
5:2mWatch next
Master Relations and Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
577
views
