Determine which functions are polynomial functions. For those that are, identify the degree.
Table of contents
- 0. Review of Algebra4h 18m
- 1. Equations & Inequalities3h 18m
- 2. Graphs of Equations1h 43m
- 3. Functions2h 17m
- 4. Polynomial Functions1h 44m
- 5. Rational Functions1h 23m
- 6. Exponential & Logarithmic Functions2h 28m
- 7. Systems of Equations & Matrices4h 5m
- 8. Conic Sections2h 23m
- 9. Sequences, Series, & Induction1h 22m
- 10. Combinatorics & Probability1h 45m
4. Polynomial Functions
Understanding Polynomial Functions
Problem 10
Textbook Question
Use the Leading Coefficient Test to determine the end behavior of the graph of the given polynomial function. Then use this end behavior to match the polynomial function with its graph. [The graphs are labeled (a) through (d).]
a.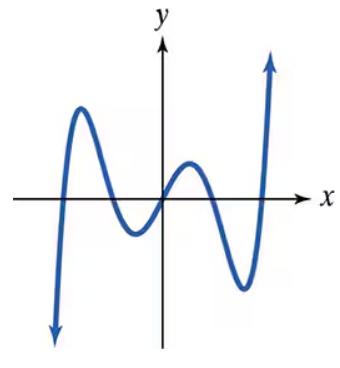 b.
b. 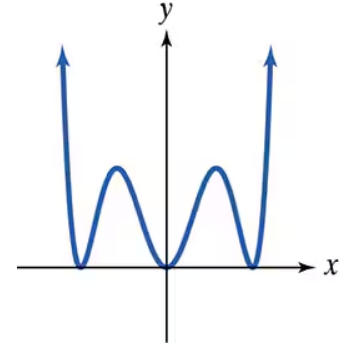 c.
c. 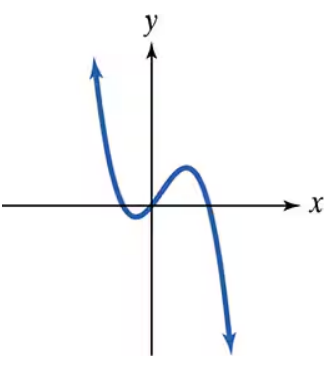 d.
d. 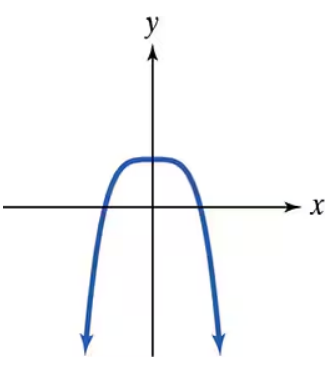
 Verified step by step guidance
Verified step by step guidance1
Identify the degree of the polynomial function \(f(x) = -x^3 + x^2 + 2x\). The degree is the highest power of \(x\), which is 3 in this case.
Determine the leading coefficient, which is the coefficient of the term with the highest degree. Here, the leading coefficient is \(-1\) (from \(-x^3\)).
Use the Leading Coefficient Test to analyze the end behavior: For an odd degree polynomial with a negative leading coefficient, as \(x \to \infty\), \(f(x) \to -\infty\), and as \(x \to -\infty\), \(f(x) \to \infty\).
Summarize the end behavior: The graph falls to the right (because \(f(x) \to -\infty\) as \(x \to \infty\)) and rises to the left (because \(f(x) \to \infty\) as \(x \to -\infty\)).
Match this end behavior with the given graphs labeled (a) through (d) by selecting the graph that shows the function rising on the left and falling on the right.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Leading Coefficient Test
The Leading Coefficient Test helps determine the end behavior of a polynomial function by examining the degree and the leading coefficient. For a polynomial f(x) = a_n x^n + ..., the sign of a_n and whether n is even or odd dictate how the graph behaves as x approaches ±∞.
Recommended video:

End Behavior of Polynomial Functions
End Behavior of Polynomial Functions
End behavior describes how the values of a polynomial function behave as x approaches positive or negative infinity. It depends on the degree and leading coefficient: odd-degree polynomials with negative leading coefficients fall to the right and rise to the left, while even-degree polynomials rise or fall on both ends.
Recommended video:

End Behavior of Polynomial Functions
Matching Polynomial Functions to Graphs
Matching a polynomial to its graph involves using the end behavior, zeros, and general shape of the function. After determining end behavior via the Leading Coefficient Test, you compare these characteristics to the given graphs to identify the correct match.
Recommended video:

Graphing Polynomial Functions

 6:04m
6:04mWatch next
Master Introduction to Polynomial Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
951
views
