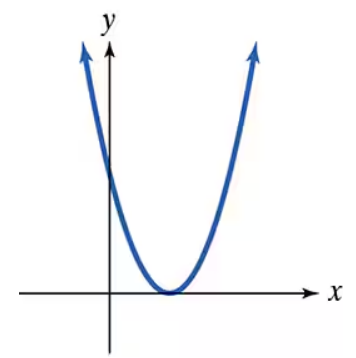
In Exercises 11–14, identify which graphs are not those of polynomial functions.

Verified step by step guidance

Step 1: Observe the graph and identify its general shape. This graph appears to be a parabola.

Step 2: Recall that a polynomial function is a function that can be written in the form f(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0, where n is a non-negative integer and the coefficients a_n, a_{n-1}, ..., a_1, a_0 are real numbers.

Step 3: Determine if the graph represents a polynomial function. A parabola is the graph of a quadratic function, which is a polynomial of degree 2.

Step 4: Check for any discontinuities, sharp corners, or vertical asymptotes. Polynomial functions are continuous and smooth, without any breaks or sharp turns.

Step 5: Conclude that the graph is indeed that of a polynomial function, specifically a quadratic function.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

50s

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Polynomial Functions

A polynomial function is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. The general form is f(x) = a_n*x^n + a_(n-1)*x^(n-1) + ... + a_1*x + a_0, where n is a non-negative integer and a_n is not zero. These functions are continuous and smooth, meaning they do not have breaks, holes, or sharp corners in their graphs.

Graph Characteristics of Polynomial Functions

The graphs of polynomial functions exhibit specific characteristics, such as being continuous and having a maximum number of turning points equal to n-1, where n is the degree of the polynomial. They can have a variety of shapes, including parabolas, but they will never cross the x-axis more times than their degree. Understanding these characteristics helps in identifying whether a given graph represents a polynomial function.

Identifying Non-Polynomial Functions

Non-polynomial functions can include rational functions, exponential functions, logarithmic functions, and trigonometric functions, which may exhibit discontinuities, asymptotes, or oscillatory behavior. To identify non-polynomial graphs, one should look for features such as sharp corners, vertical asymptotes, or discontinuities, which are not present in polynomial functions. Recognizing these traits is essential for distinguishing between polynomial and non-polynomial graphs.

Watch next

Master Introduction to Polynomial Functions with a bite sized video explanation from Patrick

Start learning