Table of contents

0. Review of Algebra4h 18m
1. Equations & Inequalities3h 18m
2. Graphs of Equations43m
3. Functions2h 17m
4. Polynomial Functions1h 44m
5. Rational Functions1h 23m
6. Exponential & Logarithmic Functions2h 28m
7. Systems of Equations & Matrices4h 6m
8. Conic Sections2h 23m
9. Sequences, Series, & Induction1h 22m
10. Combinatorics & Probability1h 45m

4. Polynomial Functions

Understanding Polynomial Functions

College Algebra

4. Polynomial Functions

Understanding Polynomial Functions

Previous problemNext problem

0:48 minutes

Problem 12

Textbook Question

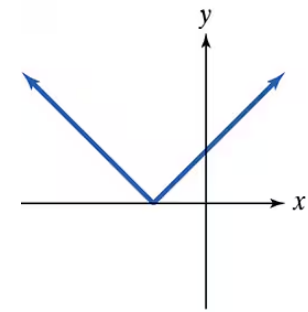
In Exercises 11–14, identify which graphs are not those of polynomial functions.

Verified step by step guidance

Observe the given graph and note its shape and characteristics.

Recall that polynomial functions are smooth and continuous curves without sharp corners or breaks.

Identify that the given graph has sharp corners, specifically at the point (5, 5).

Conclude that the presence of sharp corners indicates that the graph is not a polynomial function.

Therefore, determine that this graph is not the graph of a polynomial function.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

48s

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Polynomial Functions

Polynomial functions are mathematical expressions that consist of variables raised to non-negative integer powers, combined using addition, subtraction, and multiplication. They can be represented in the form f(x) = a_n*x^n + a_(n-1)*x^(n-1) + ... + a_1*x + a_0, where a_n, a_(n-1), ..., a_0 are constants and n is a non-negative integer. The graph of a polynomial function is continuous and smooth, without any sharp corners or breaks.

Characteristics of Non-Polynomial Functions

Non-polynomial functions can exhibit various characteristics that distinguish them from polynomial functions. These may include sharp corners, discontinuities, or asymptotic behavior. For example, absolute value functions, piecewise functions, and rational functions can have such features, making their graphs non-smooth or non-continuous at certain points.

Graph Interpretation

Interpreting graphs involves analyzing the visual representation of mathematical functions to identify their properties and behaviors. Key aspects include recognizing shapes, identifying intercepts, and determining continuity or discontinuity. In the context of polynomial functions, a graph that displays sharp turns or breaks indicates that it is not a polynomial, as polynomial graphs are characterized by their smooth curves.