Write an equation (a) in standard form and (b) in slope-intercept form for each line described. through (-1, 4), parallel to x+3y=5

The standard form of a linear equation is expressed as Ax + By = C, where A, B, and C are integers, and A should be non-negative. This form is useful for easily identifying the x- and y-intercepts of the line. To convert from slope-intercept form (y = mx + b) to standard form, you can rearrange the equation to fit the Ax + By = C format.

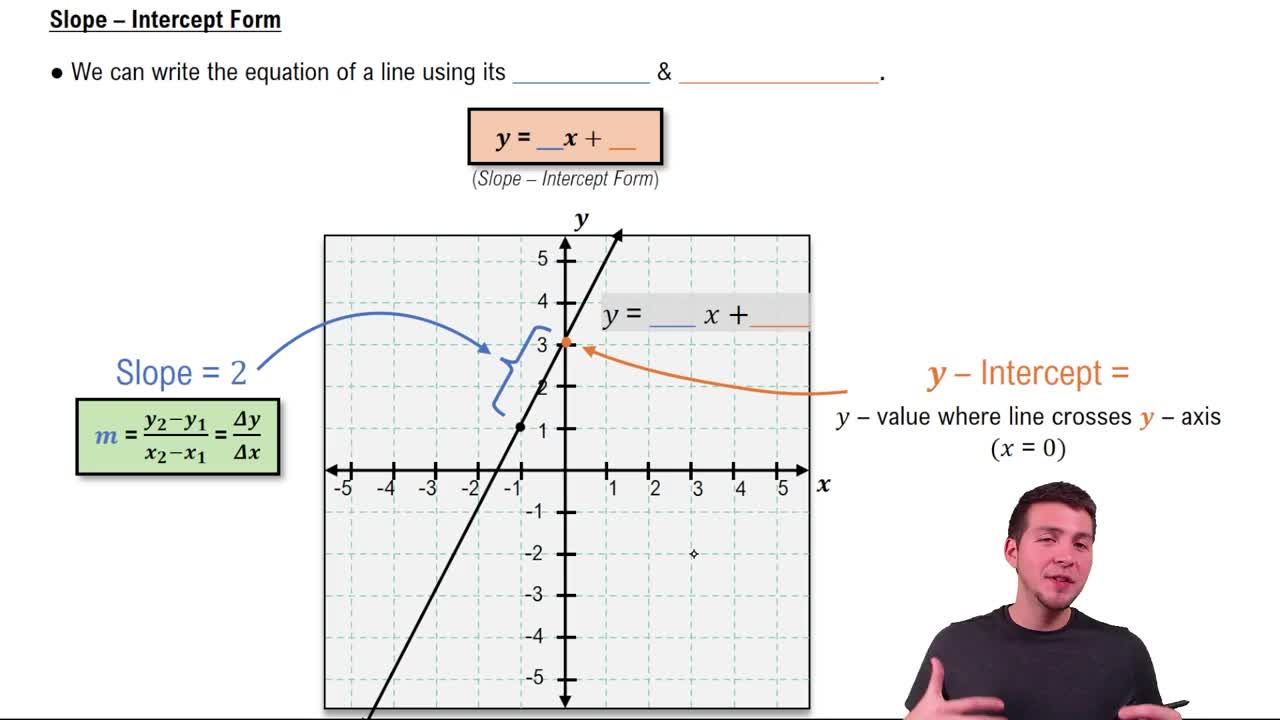
The slope-intercept form of a linear equation is given by y = mx + b, where m represents the slope of the line and b is the y-intercept. This form is particularly useful for quickly graphing the line, as it directly provides the slope and where the line crosses the y-axis. Understanding how to manipulate this form is essential for solving problems involving linear equations.

Two lines are parallel if they have the same slope but different y-intercepts. In the context of linear equations, if a line is parallel to another, it will not intersect it at any point. To find the equation of a line parallel to a given line, you can use the slope of the original line and the coordinates of a point through which the new line passes to derive its equation.