Begin by graphing f(x) = log₂ x. Then use transformations of this graph to graph the given function. What is the vertical asymptote? Use the graphs to determine each function's domain and range. h(x) = 2 + log₂x

In Exercises 53-58, begin by graphing f(x) = log₂ x. Then use transformations of this graph to graph the given function. What is the vertical asymptote? Use the graphs to determine each function's domain and range. g(x) = (1/2)log₂ x

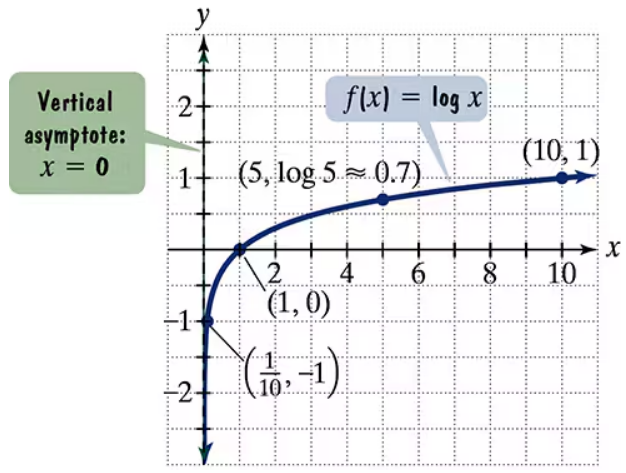
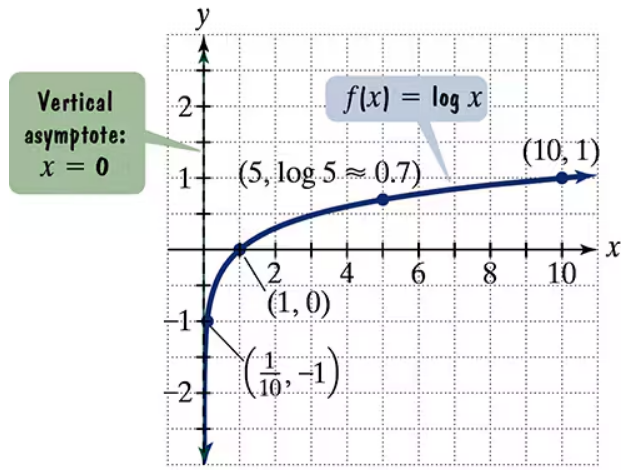
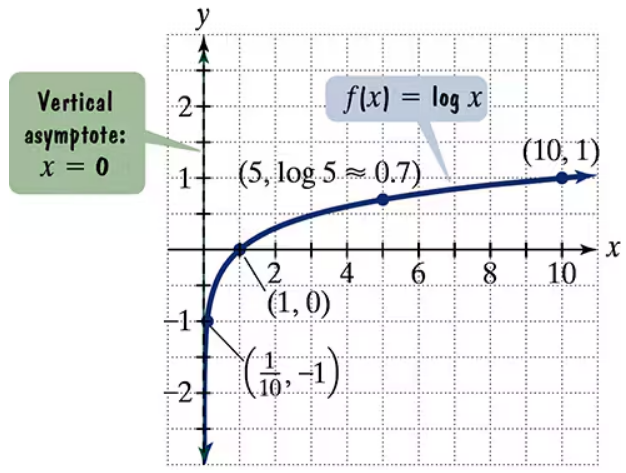
The figure shows the graph of f(x) = log x. In Exercises 59–64, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. g(x) = log(x − 1)

The figure shows the graph of f(x) = log x. In Exercises 59–64, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. h(x) = log x − 1

The figure shows the graph of f(x) = log x. In Exercises 59–64, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range.

g(x) = 1-log x

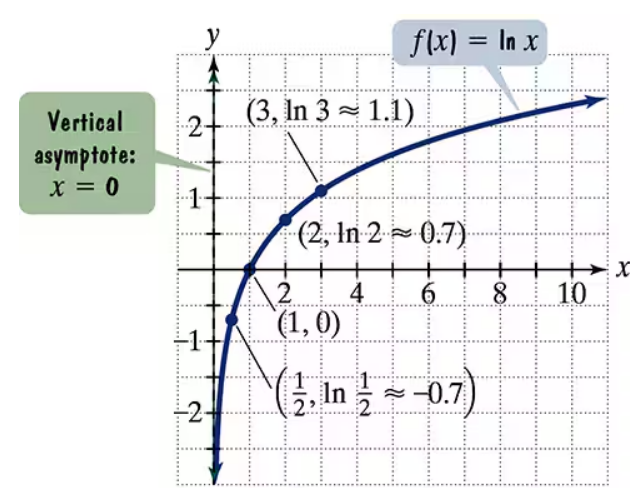
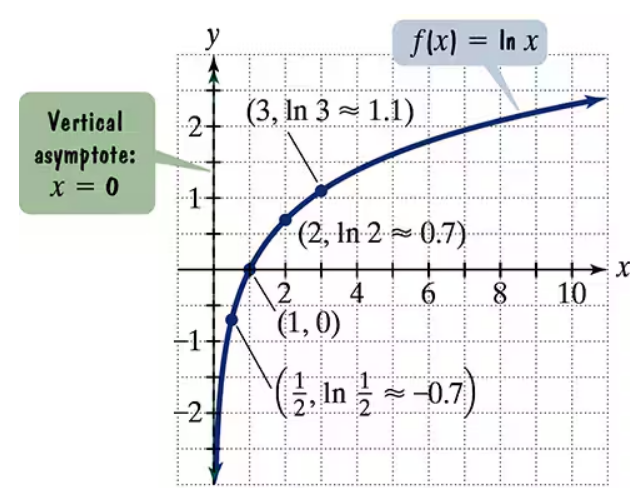
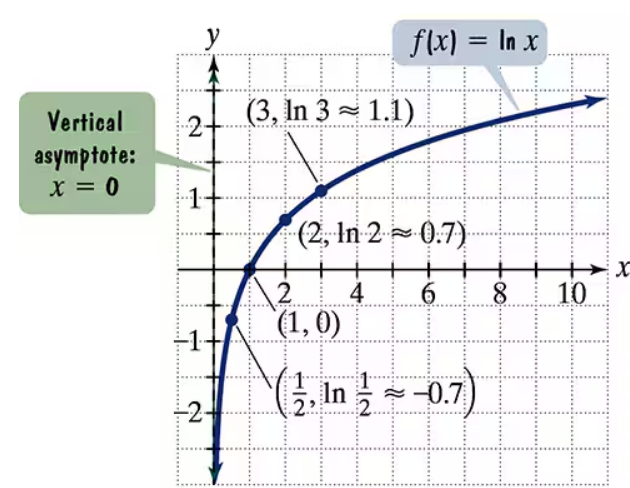
The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. g(x) = ln (x+2)

The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range.

h(x) = ln (2x)

The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. h(x) = ln(x/2)

The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. g(x) = 2 ln x

Find the domain of each logarithmic function. f(x) = log₅(x+4)

Find the domain of each logarithmic function. f(x) = log (2 - x)

Find the domain of each logarithmic function. f(x) = ln (x-2)²

Evaluate or simplify each expression without using a calculator. log 100

Evaluate or simplify each expression without using a calculator. log 10⁷

Evaluate or simplify each expression without using a calculator. 10^{log 33}

Evaluate or simplify each expression without using a calculator. In 1

Evaluate or simplify each expression without using a calculator. In e

Evaluate or simplify each expression without using a calculator. In e⁶

Evaluate or simplify each expression without using a calculator. In (1/e⁶)

Evaluate or simplify each expression without using a calculator. e^{ln 125}

Evaluate or simplify each expression without using a calculator. In e^9x

Evaluate or simplify each expression without using a calculator. $e^{\ln 5x^2}$

Evaluate or simplify each expression without using a calculator. 10^{log √x}

Evaluate or simplify each expression without using a calculator. 10^{log ∛x}

Write each equation in its equivalent exponential form. Then solve for x. log₃ (x-1) = 2

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log₅ (7 × 3)

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log₇ (7x)

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log(1000x)

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log₇ (7/x)

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log(x/100)