[APPLET] The waking times (in minutes past 5:00 A.M.) of 40 people who start work at 8:00 A.M. are shown in the table at the left. Assume the population standard deviation is 45 minutes. Find (a) the point estimate of the population mean μ and (b) the margin of error for a 90% confidence interval.
Table of contents
- 1. Intro to Stats and Collecting Data55m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically1h 45m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables2h 33m
- 6. Normal Distribution and Continuous Random Variables1h 38m
- 7. Sampling Distributions & Confidence Intervals: Mean1h 53m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample2h 19m
- 10. Hypothesis Testing for Two Samples3h 22m
- 11. Correlation1h 6m
- 12. Regression1h 4m
- 13. Chi-Square Tests & Goodness of Fit1h 20m
- 14. ANOVA1h 0m
7. Sampling Distributions & Confidence Intervals: Mean
Confidence Intervals for Population Mean
Problem 6.R.7
Textbook Question
Determine the minimum sample size required to be 95% confident that the sample mean waking time is within 10 minutes of the population mean waking time. Use the population standard deviation from Exercise 1.
 Verified step by step guidance
Verified step by step guidance1
Identify the formula for determining the minimum sample size for estimating a population mean: , where is the sample size, is the z-score corresponding to the confidence level, is the population standard deviation, and is the margin of error.
Determine the z-score for a 95% confidence level. For a 95% confidence level, the z-score corresponds to the critical value where the cumulative probability is 0.975 (since 95% confidence leaves 2.5% in each tail).
Substitute the given margin of error, minutes, into the formula. This represents the maximum allowable difference between the sample mean and the population mean.
Use the population standard deviation from Exercise 1, denoted as , and substitute it into the formula. Ensure the units are consistent (e.g., minutes).
Calculate the value of by squaring the result of . Round up to the nearest whole number, as sample size must be an integer.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Sample Size Determination
Sample size determination is the process of calculating the number of observations or replicates needed in a statistical study to achieve a desired level of confidence and precision. In this context, it involves using the desired margin of error, confidence level, and population standard deviation to find the minimum sample size that ensures the sample mean is within a specified range of the population mean.
Recommended video:
Guided course

Coefficient of Determination
Confidence Level
The confidence level represents the probability that the confidence interval calculated from the sample data will contain the true population parameter. A 95% confidence level indicates that if the same sampling procedure were repeated multiple times, approximately 95% of the calculated intervals would capture the true population mean, providing a strong assurance of the reliability of the results.
Recommended video:

Introduction to Confidence Intervals
Margin of Error
The margin of error is the range within which the true population parameter is expected to lie, given a certain level of confidence. In this scenario, a margin of error of 10 minutes means that the sample mean waking time should be within 10 minutes of the actual population mean. This concept is crucial for determining how precise the estimate needs to be and directly influences the required sample size.
Recommended video:
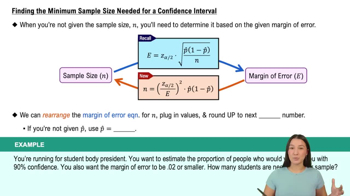
Finding the Minimum Sample Size Needed for a Confidence Interval

 4:48m
4:48mWatch next
Master Population Standard Deviation Known with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
19
views
