In Exercises 5 and 6, use the confidence interval to find the margin of error and the sample mean.
(20.75, 24.10)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: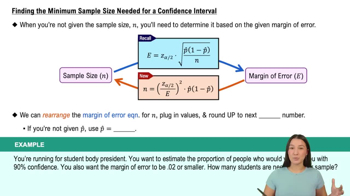



 4:48m
4:48mMaster Population Standard Deviation Known with a bite sized video explanation from Patrick
Start learning