True or False: Sample evidence can prove a null hypothesis is true.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 25m
- 9. Hypothesis Testing for One Sample3h 57m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 24m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit2h 21m
- 14. ANOVA1h 57m
9. Hypothesis Testing for One Sample
Performing Hypothesis Tests: Proportions
Struggling with Statistics?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
Perform a 2-tailed hypothesis test for the true proportion of successes using the given values:
, , , & claim is
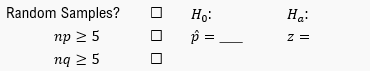
A
Because P-value = 0.00004 < α= 0.01, we FAIL TO REJECT H0. There is NOT ENOUGH evidence to suggest Ha: p ≠ 0.75
B
Because P-value = 0.00004 < α= 0.01, we REJECT H0. There is ENOUGH evidence to suggest Ha: p ≠ 0.75
C
Because P-value = 0.00008 < α= 0.01, we REJECT H0. There is ENOUGH evidence to suggest Ha: p ≠ 0.75
D
Because P-value = 0.00008 < α= 0.01, we FAIL TO REJECT H0. There is NOT ENOUGH evidence to suggest Ha: p ≠ 0.75
 Verified step by step guidance
Verified step by step guidance1
Step 1: Define the null hypothesis (H₀) and the alternative hypothesis (Hₐ). The null hypothesis is H₀: p = 0.25, and the alternative hypothesis is Hₐ: p ≠ 0.25, since this is a two-tailed test.
Step 2: Calculate the sample proportion (p̂). The formula for p̂ is p̂ = x / n, where x is the number of successes (42) and n is the sample size (100).
Step 3: Verify the conditions for performing a hypothesis test for proportions. Ensure that both np and nq are greater than or equal to 5, where q = 1 - p. For np, calculate np = n * p, and for nq, calculate nq = n * q.
Step 4: Compute the test statistic (z-value). The formula for the z-value is z = (p̂ - p) / √(p * q / n), where p̂ is the sample proportion, p is the claimed proportion, q = 1 - p, and n is the sample size.
Step 5: Compare the calculated z-value to the critical z-value for α = 0.10 (two-tailed test) or use the p-value approach. If the p-value is less than α, reject the null hypothesis; otherwise, fail to reject the null hypothesis.

 5:52m
5:52mWatch next
Master Performing Hypothesis Tests: Proportions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
10
views
Performing Hypothesis Tests: Proportions practice set


