"Simulation Simulate drawing 100 simple random samples of size n = 40 from a population whose proportion is 0.3.
d. How do we know that a rejection of the null hypothesis results in making a Type I error in this situation?"
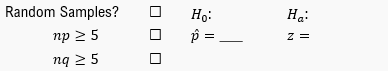
Because -value = 0.465 > 0.01, we FAIL TO REJECT . There is NOT ENOUGH evidence to suggest : ≠ 0.75
Because P-value = 0.465 > α= 0.01, we REJECT . There is ENOUGH evidence to suggest Ha: p ≠ 0.75
Because P-value = 0.233 > α= 0.01, we REJECT H0. There is ENOUGH evidence to suggest Ha: p ≠ 0.75
Because P-value = 0.233 > α= 0.01, we FAIL TO REJECT H0. There is NOT ENOUGH evidence to suggest Ha: p ≠ 0.75
 Verified step by step guidance
Verified step by step guidance
 5:52m
5:52mMaster Performing Hypothesis Tests: Proportions with a bite sized video explanation from Patrick
Start learning
