A company’s marketing team takes 50 samples of 10 recent clients to create a sampling distribution of sample means for the average amount spent per month on company products. Can the Central Limit Theorem be used to determine that the sampling distribution is normal?
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion2h 10m
- 9. Hypothesis Testing for One Sample5h 8m
- Steps in Hypothesis Testing1h 6m
- Performing Hypothesis Tests: Means1h 4m
- Hypothesis Testing: Means - Excel42m
- Performing Hypothesis Tests: Proportions37m
- Hypothesis Testing: Proportions - Excel27m
- Performing Hypothesis Tests: Variance12m
- Critical Values and Rejection Regions28m
- Link Between Confidence Intervals and Hypothesis Testing12m
- Type I & Type II Errors16m
- 10. Hypothesis Testing for Two Samples5h 37m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- Two Variances and F Distribution29m
- Two Variances - Graphing Calculator16m
- 11. Correlation1h 24m
- 12. Regression3h 33m
- Linear Regression & Least Squares Method26m
- Residuals12m
- Coefficient of Determination12m
- Regression Line Equation and Coefficient of Determination - Excel8m
- Finding Residuals and Creating Residual Plots - Excel11m
- Inferences for Slope31m
- Enabling Data Analysis Toolpak1m
- Regression Readout of the Data Analysis Toolpak - Excel21m
- Prediction Intervals13m
- Prediction Intervals - Excel19m
- Multiple Regression - Excel29m
- Quadratic Regression15m
- Quadratic Regression - Excel10m
- 13. Chi-Square Tests & Goodness of Fit2h 21m
- 14. ANOVA2h 28m
7. Sampling Distributions & Confidence Intervals: Mean
Sampling Distribution of the Sample Mean and Central Limit Theorem
Problem 5.4.24
Textbook Question
Interpreting the Central Limit Theorem In Exercises 19–26, find the mean and standard deviation of the indicated sampling distribution of sample means. Then sketch a graph of the sampling distribution.
Salaries The annual salaries for web software development managers are normally distributed, with a mean of about \$136,000 and a standard deviation of about \$11,500. Random samples of 40 are drawn from this population, and the mean of each sample is determined.
 Verified step by step guidance
Verified step by step guidance1
Identify the population mean (\$\mu\$) and population standard deviation (\$\sigma\$). Here, \$\mu = 136,000\$ and \$\sigma = 11,500\$.
Note the sample size \$n = 40\$ and recognize that the sampling distribution of the sample mean will have its own mean and standard deviation.
Calculate the mean of the sampling distribution of the sample mean, which is the same as the population mean: \$\mu_{\bar{x}} = \mu = 136,000\$.
Calculate the standard deviation of the sampling distribution of the sample mean (also called the standard error) using the formula: \$\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}} = \frac{11,500}{\sqrt{40}}\$.
Since the population distribution is normal, the sampling distribution of the sample mean will also be normal. Sketch a normal curve centered at \$136,000\$ with spread determined by \$\sigma_{\bar{x}}\$.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
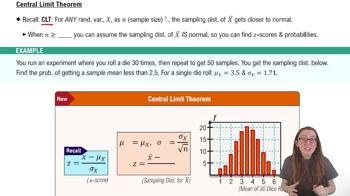
Central Limit Theorem (CLT)
The Central Limit Theorem states that the sampling distribution of the sample mean approaches a normal distribution as the sample size becomes large, regardless of the population's distribution. For sample sizes typically greater than 30, the sample means will be approximately normally distributed, enabling inference about the population mean.
Recommended video:
Central Limit Theorem
Sampling Distribution of the Sample Mean
The sampling distribution of the sample mean is the probability distribution of all possible sample means from samples of a fixed size. It has a mean equal to the population mean and a standard deviation (standard error) equal to the population standard deviation divided by the square root of the sample size.
Recommended video:

Sampling Distribution of Sample Mean
Standard Error of the Mean
The standard error measures the variability of the sample mean from the population mean. It is calculated as the population standard deviation divided by the square root of the sample size, reflecting how much sample means fluctuate around the true mean in repeated sampling.
Recommended video:
Guided course

Calculating the Mean

 6:53m
6:53mWatch next
Master Sampling Distribution of Sample Mean with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
130
views
