Performing a One-Way ANOVA Test In Exercises ...

Question

Performing a One-Way ANOVA Test In Exercises 5–14, (a) identify the claim and state H0 and Ha, (b) find the critical value and identify the rejection region, (c) find the test statistic F, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, the populations are normally distributed, and the population variances are equal.

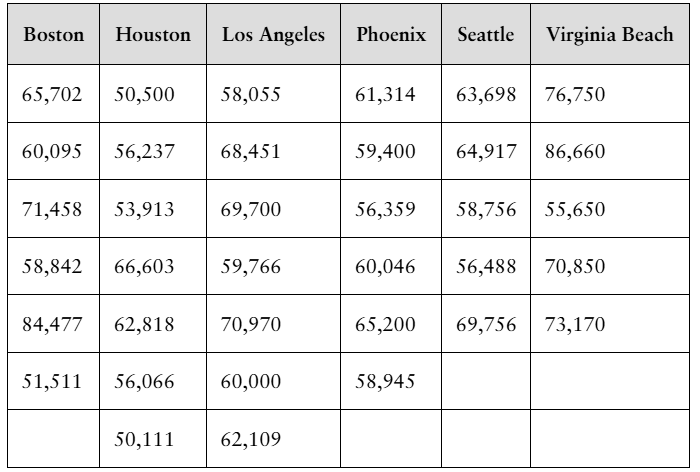
[APPLET] Statistician Salaries The table shows the salaries of a sample of entry level statisticians from six large metropolitan areas. At α=0.05, can you conclude that the mean salary is different in at least one of the areas? (Adapted from Salary.com)

[APPLET] Statistician Salaries The table shows the salaries of a sample of entry level statisticians from six large metropolitan areas. At α=0.05, can you conclude that the mean salary is different in at least one of the areas? (Adapted from Salary.com)

Accepted Answer

Hello there. Today we're gonna solve the following practice problem together. So, first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. A tech recruiter is analyzing the starting salaries in units of US dollars of entry-level software engineers in six major US cities to determine whether location influences pay. Salaries were collected from a random sample of 5 job offers in each of the following cities San Francisco, Austin, New York, Denver, Chicago, and Atlanta. The mean square between groups MSB is. 10523,283.34. And the mean square within groups, MSW is 2,976,333.33. Add alpha equals 0.05, can you conclude that the mean starting salary differs for at least one of the cities? Awesome. So it appears for this particular problem, we're asked to focus on a specific level of significance of 0.05. We're asked if we can conclude that the mean starting salary differs for at least 1. Of the cities listed by the prom itself. So ultimately we're taking all the information that is provided to us by the prom itself, and we're trying to determine whether or not we can conclude that the mean starting salary differs for at least one of the cities mentioned. So with that in mind, let's read off our multiple choice answers to see what our final answer might be. A is no. The mean starting salaries are equal across all six cities. B is the test fails due to small sample size in each group. C is yes, there is sufficient evidence to suggest at least one city has a different average starting salary. And is there is not enough information to perform the ANOVA test. Awesome. So, with that in mind, let's take a moment to write down all the information that is provided to us by the prom itself. So once again, we're told that MSB is equal to 105 million. 23,283.34 and we're told that MSW is equal to 2,976,333.33. We're told that K is equal to 6, where K denotes our cities, and we have 6 different cities, and we're told that alpha, our level of significance, is equal to 0.05. Fantastic. So with that in mind, our first step that we need to take in order to solve this problem is we need to state our hypotheses, starting with the null hypothesis, which will denote as H0. So our null hypothesis, as we should recall and be able to recognize, will be the mean starting salaries are all the same for all the cities. So once again, the mean starting salaries are the same for all cities. That will be our no hypothesis. And for our alternative hypothesis, HA, at least one city's mean salary differs. So once again, to reiterate, since this is very important to note, for our null hypothesis, the mean starting salaries are the same for all cities, whereas for our alternative hypothesis, at least one city's mean salary differs. So with that in mind, Our next step now, since now that we've stated our hypotheses, our next step now is we need to compute the F statistic. So as you should recall, the F statistic, which we'll call F, is equal to MSB divided by MSW, which is equal to when we plug in our known variables, 10523,283.34. And we need to divide this value by. 2,976,333.33. And when we plug this expression into our calculator, we will find that it's simply equal to 35.29 when we round to two decimal places. Fantastic. So now, our third step. we need to make our final decision. So we need to note that our critical F value, which I'll call F subscript C, so for our F critical value, and once again, we're focusing on the level of significance alpha being 0.05 means that's very important when determining our F. Our F value, when we're trying to find our critical F value, we need to pay attention to what the level of significance is. And we're also told that our degrees of freedom one, so DF1. is equal to K minus 1, and minus 1 will be equal to 6 minus 1, which is equal to 5. And for our degrees of freedom, 2, which we'll call DF2, will be equal to N minus K, which is equal to 30, minus 6, which is equal to 24. And based on this information, because once again, in order to determine our critical F value, we need to know the degrees of freedom, and we need to know the level of significance. And when we take all that information into account for this particular problem, you will determine that FC, or critical F value for this particular problem, will be equal to 2.621. And now, with that in mind since F is equal to 35.29, which is greater than 2.621. So once again, because F, our F value is greater than our critical F value, we can therefore reject the null hypothesis. So I put an X next to H0. So once again, because 35.29 is greater than 2.621, we can reject the null hypothesis, and because we can reject the null hypothesis, we can make the final conclusion. There is strong evidence at the 0.05 significance level that means starting salaries differ for at least one city. So that will mean when we look at our multiple choice answers, the correct answer without a doubt will have to be multiple choice answer letter C, which once again is yes, there is sufficient evidence to suggest that at least one city has a different average starting salary. And that's it. That's our final answer. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

Key Concepts

One-Way ANOVA Test

Hypothesis Testing and Rejection Region

F-Statistic Calculation and Interpretation

Watch next