Finding the Margin of Error In Exercises 33 and 34, use the confidence interval to find the estimated margin of error. Then find the sample mean. Book Prices A store manager reports a confidence interval of (244.07, 280.97) when estimating the mean price (in dollars) for the population of textbooks.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 25m
- 9. Hypothesis Testing for One Sample3h 57m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 24m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit2h 21m
- 14. ANOVA1h 57m
7. Sampling Distributions & Confidence Intervals: Mean
Confidence Intervals for Population Mean
Problem 6.1.43b
Textbook Question
When all other quantities remain the same, how does the indicated change affect the width of a confidence interval? Explain.
b. Increase in the sample size
 Verified step by step guidance
Verified step by step guidance1
Understand the relationship between sample size and the width of a confidence interval: The width of a confidence interval is inversely related to the square root of the sample size. This means that as the sample size increases, the width of the confidence interval decreases.
Recall the formula for the margin of error in a confidence interval: \( \text{Margin of Error} = z^* \cdot \frac{\sigma}{\sqrt{n}} \), where \( z^* \) is the critical value, \( \sigma \) is the population standard deviation, and \( n \) is the sample size.
Analyze the effect of increasing the sample size \( n \): Since \( n \) appears in the denominator under a square root, increasing \( n \) will decrease the value of \( \frac{\sigma}{\sqrt{n}} \), which in turn reduces the margin of error.
Conclude how this impacts the confidence interval: A smaller margin of error results in a narrower confidence interval, meaning the range of values within which the population parameter is estimated becomes more precise.
Summarize the effect: Increasing the sample size reduces the width of the confidence interval, improving the precision of the estimate while keeping all other factors constant.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Confidence Interval
A confidence interval is a range of values, derived from sample statistics, that is likely to contain the true population parameter. It is expressed with a certain level of confidence, typically 95% or 99%, indicating the degree of certainty about the estimate. The width of the interval reflects the precision of the estimate; narrower intervals suggest more precise estimates.
Recommended video:

Introduction to Confidence Intervals
Sample Size
Sample size refers to the number of observations or data points collected in a study. A larger sample size generally leads to more reliable estimates of population parameters, as it reduces the impact of random variability. In the context of confidence intervals, increasing the sample size typically results in a narrower interval, indicating greater precision in estimating the population parameter.
Recommended video:

Sampling Distribution of Sample Proportion
Margin of Error
The margin of error is the amount of error that can be tolerated in the estimate of a population parameter. It is influenced by the sample size and the variability of the data. A larger sample size decreases the margin of error, which in turn reduces the width of the confidence interval, allowing for a more accurate representation of the population parameter.
Recommended video:
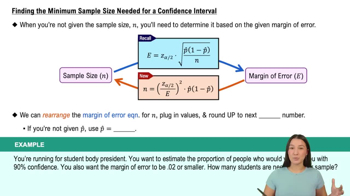
Finding the Minimum Sample Size Needed for a Confidence Interval

 4:48m
4:48mWatch next
Master Population Standard Deviation Known with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
27
views
