In Exercises 9–12, find the critical value tc for the level of confidence c and sample size n.
c = 0.98, n = 15
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: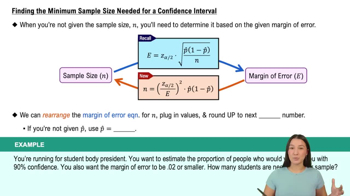



 4:48m
4:48mMaster Population Standard Deviation Known with a bite sized video explanation from Patrick
Start learning