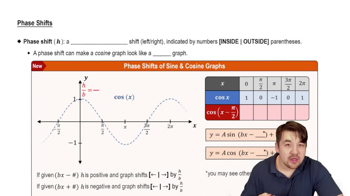
For each function, give the amplitude, period, vertical translation, and phase shift, as applicable.
y = 3 cos (x + π/2)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 5:53m
5:53mMaster Graph of Sine and Cosine Function with a bite sized video explanation from Patrick
Start learning